平行四辺形 証明 解き方
有名な 平行四辺形 証明 解き方 平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方.
平行四辺形 証明 解き方. 平行四辺形の証明問題の解き方について説明します。ポイントはこちら↓ ポイント 四角形が平行四辺形になる条件(5つ. 中学の数学での図形の証明問題は合同か相似を利用することがほとんどです。 長さが等しいことや角度が等しいことを証明するには合同か相似を証明してからになります。 ここでは図形の証明問題の解き方と証明の書き方のポイントをお伝え …. 数学・算数 - 中学2年の子供の母親です。 子供の夏休みの宿題の答え合わせをしているのですが、恥ずかしながら、画像の問題の解き方がわかりません。 どのような証明をすれば良いか、教えていただきたく、よろ.
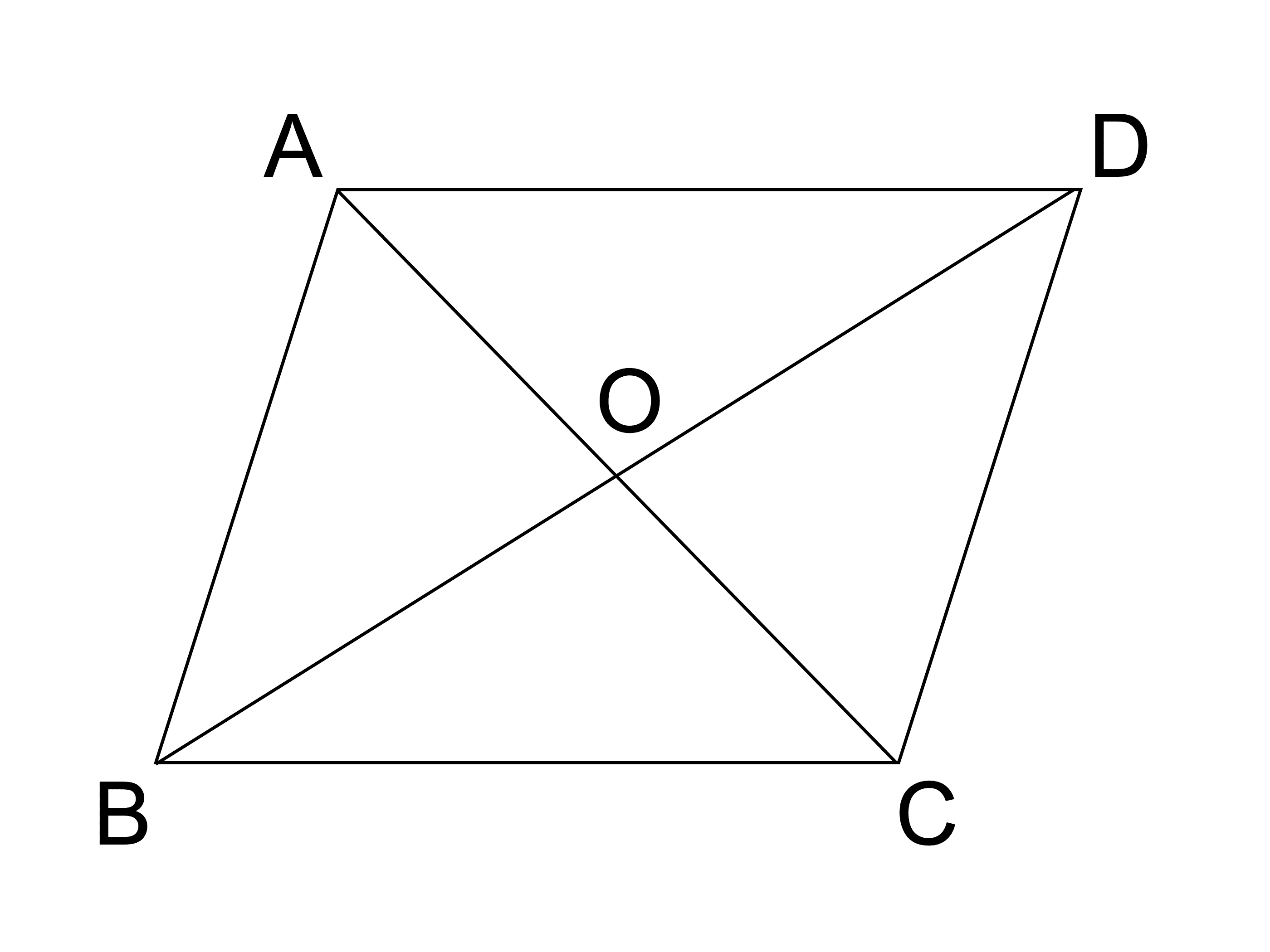
中学校 - 数学の証明問題の解き方 今,中学二年生なのですが『証明問題』が分からないんです。三角形の合同条件とか平行四辺形の合同条件などは分かるんです。 でもその解き方っていうかやり方がわからないんで. さて、昨日に引き続き証明のコツの続き。 実際に問題を解きながらお話しします。 ちなみに、 この問題はテストによく出題される問題なので、必ずできるようにしておきましょう 。 問題 abcdで、上の図のように、対角線の交点oを通る直線をひき、2辺ab、cdとの交点を、それぞれp、qとします。. 中学2年で学習する「平行と合同」単元のポイントまとめと証明のしかた、書き方をお伝えします。 中学2年生でテストで得点が下がる人が急増するのがこの「平行と合同」分野です。 角度の問題は計算できれば良いですが、大切な用語が増 ….
平行四辺形を利用した証明についての質問です。 この画像の平行四辺形abcdのcdの中点をeとし、aからbeに引いた垂線のbeとの交点をfとした時 da=dfを証明せよ という問題なのですが、解き方が分からず困っていま. 平行四辺形になるための証明1 4解説 (4) 図の abcdで∠bae=∠dcfのとき四角形aecfが平行四辺形となることを証明せよ。 a b c d e f. 最高の平行四辺形 証明 解き方 epa erliani | 年10月1日木曜日 平行四辺形の証明の解き方を教えて欲しいです Yahoo 知恵袋.
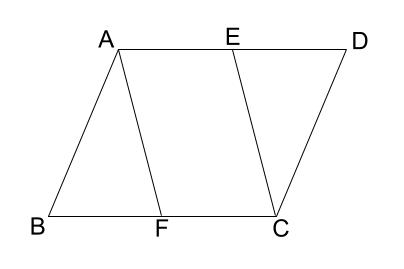
右は(1)で見つけた 21:7(3:1) または 8分の3 : 8分の1 (3:1)を使って 平行四辺形の4分の1を分けてー♪。 こちらは時間差はあまりありません。 が. 略した証明〉 ad 上にそれぞれ点じ,fを, be一df となるよう cf であることを夏功しなさい。. 一般四角形から正四角形へ全ての四角形を使って進化させる方法を教えてください。四角形 1組の向かい合う辺を平行にする台形 2組の向かい合う辺を平行にする平行四辺形 隣り合う内角の大きさを等しくする.
「数学。証明問題、解き方と記述のコツ!その1」の中で、 証明問題は3ステップの順番で 問題に取り組むというお話をしました。 今回はその続きで、 ステップ3の ③証明の記述を行っていく からお話をしていきます。 前回の記事を読んでいない人は. 今日は、前回の田庭の平行四辺形のブログに便乗して、苦手克服パート2です。 「 abdと aceが合同であることを証明しなさい。」 「 acmと aemが相似であることを証明しなさい。」 こう聞くと後に回そうと思う人は多いのではないでしょうか?. この記事では、中点連結定理について、証明や定理の逆や応用についてわかりやすく解説していきます。 また、問題の解き方も簡単に解説していくので、ぜひこの記事を通してマスターしてくださいね! 目次中点連結定理とは?中点連結.
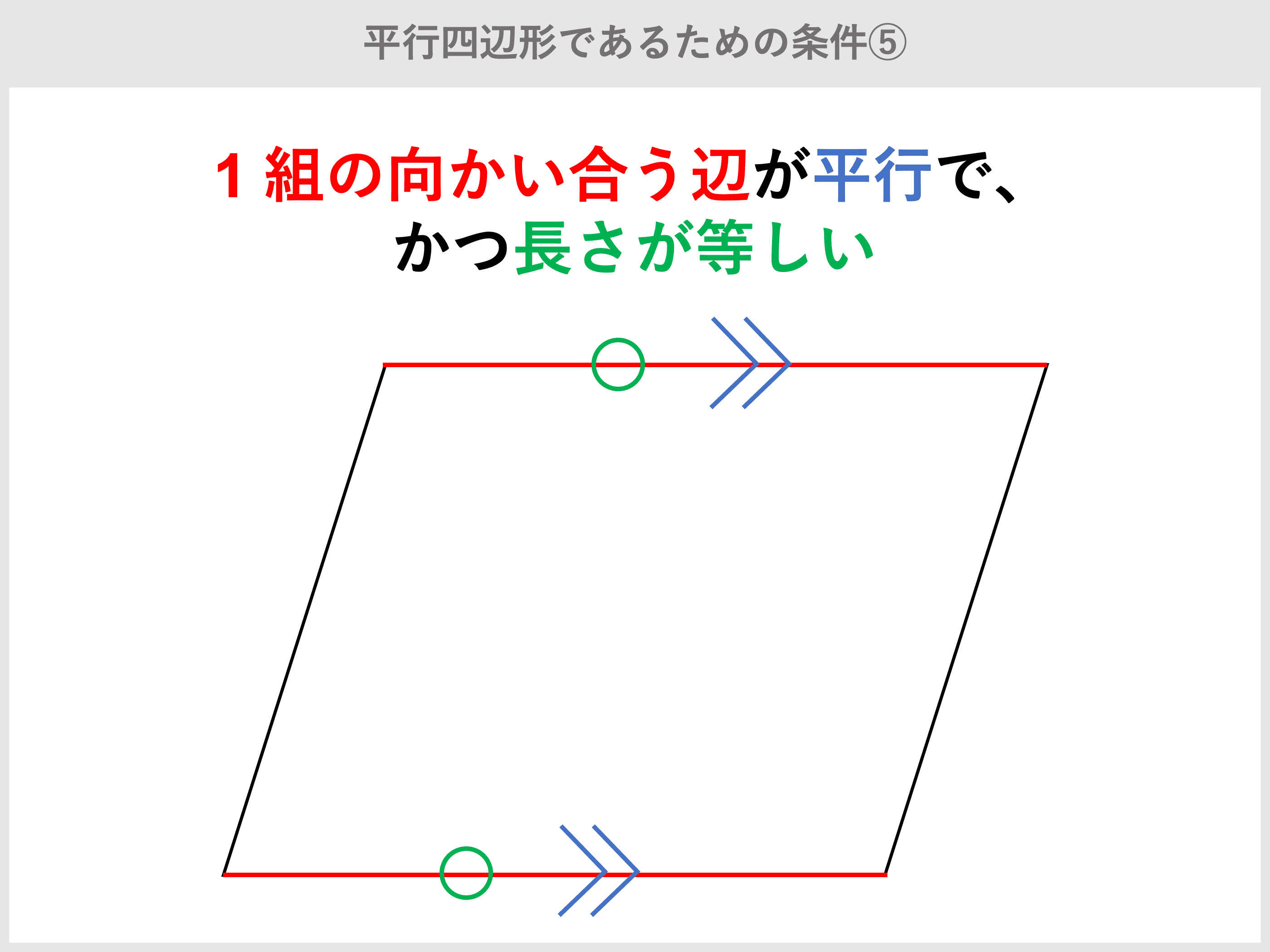
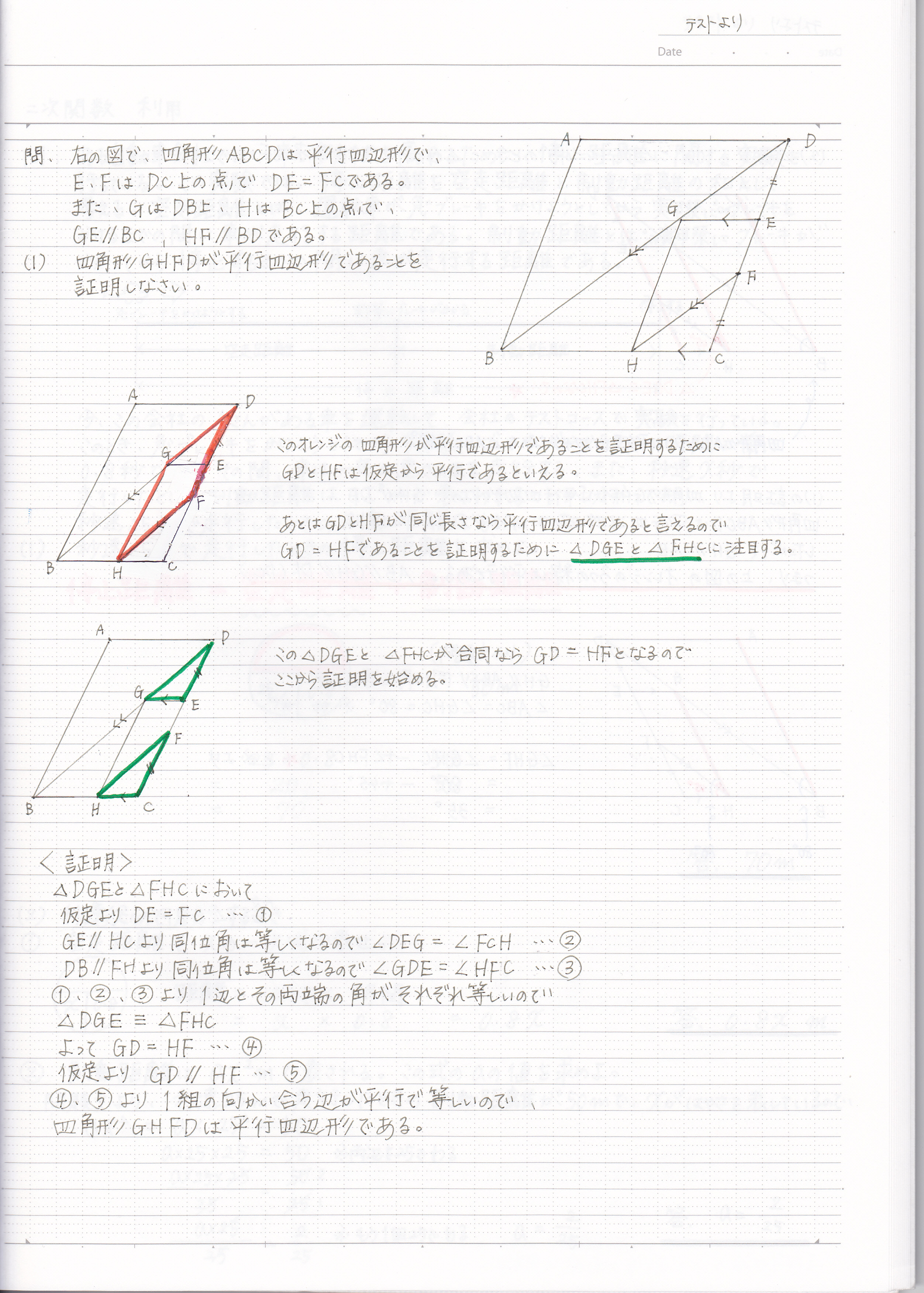
このとき四角形afbdが平行四辺形となることを証明せよ。 図で、 abcの辺ab上に点dがあり、 辺acの中点をmとする。dmの延長上にdm=emとなる点eを取る。このとき四角形adceは平行四辺形となることを証明せよ。 abcdで∠abe=∠cdfのとき四角形ebfdが平行四辺形になる. この5つは平行四辺形であるための条件として,文言をそのまま覚えましょう。三角形の合同条件と同じように,証明問題ではこの文言が必要となります。 関連記事 「平行四辺形の性質」について詳しく知りたい方はこちら 「平行四辺形,長方形,ひし形,正方形の違い」について詳しく知り. 平行四辺形abcdで, 対角線の交点oを通る直線を,右の図のようにひき, 2辺ab, cd との交点を, それぞれ, p, q とします。このとき, op=oq となることを証明しなさい。 解答3.
中2数学。2つの「辺の長さ」が等しいことを証明せよ。ヤバい…これも合同証明? それとも違うの? 図形はムズカシイ…(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 証明問題はコツがある!(ビシッ)無料サイトだ。. この頁では平行線の性質について,1つの性質から他の性質を証明する場合を例にとって,仮定と結論の選び方を練習する.(仮定と結論が分かれば証明の入口と出口が分かるので,これにそって実際の証明を考えていくことになる.) 例1 「平行四辺形で. 計量 73 データの分析 44 数学a 226 場合の数と確率 116 整数の性質 80 図形の性質 30 数学ii 399 式と証明 74 複素数と方程式 35 図形と.
中学数学 証明 平行四辺形の性質の利用 中学数学の無料学習サイト. 数学 - 中学2年の子供の母親です。 子供の夏休みの宿題の答え合わせをしているのですが、恥ずかしながら、画像の問題の解き方がわかりません。 どのような証明をすれば良いか、教えていただきたく、よろしくお. 言い忘れてましたが、三角形と比の定理も 全く同じ方法 で証明ができます。 これが、冒頭で「この $2$ つの定理を区別する必要は.
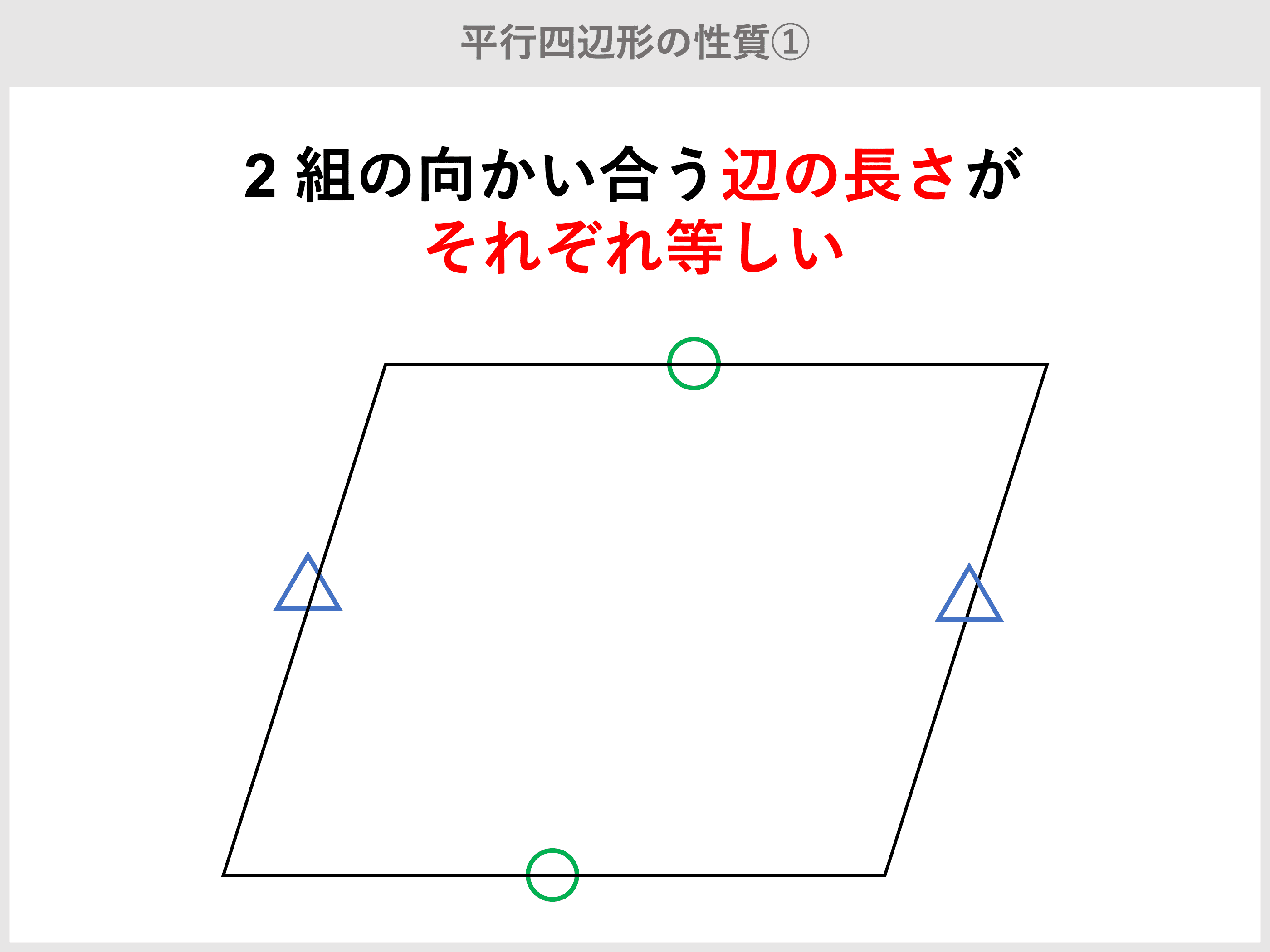
平行四辺形の定義と性質・証明問題の解き方 管理人 2月 23, 19 平行四辺形の性質で角度を求めたり、平行四辺形であることを証明したりする問題がよく出されます。. 平行四辺形の性質 証明の問題に、平行四辺形がでてくることがあります。 このとき、平行四辺形には以下の \(4\) つが成り立っていることは 暗黙の前提です。証明なしで使って構いません。 ・\(2\) 組の対辺がそれぞれ平行 ・\(2\) 組の対辺がそれぞれ等しい ・\(2\) 組の対角がそれぞれ等しい. この記事では、ベクトルの平行条件や垂直条件について、できるだけわかりやすく解説していきます。 計算問題だけでなく、証明問題の解き方も解説していきますので、この記事を通してぜひマスターしてくださいね。 目次ベクトルの.
平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典

数学の証明問題 中学数学に関する質問 勉強質問サイト
まとめるノート 中2数学
平行四辺形 証明 解き方 のギャラリー

平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を抑えよう 遊ぶ数学
平行四辺形であることを証明する 苦手な数学を簡単に

平行四辺形を使った証明 Youtube
特別な平行四辺形2
中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su

平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題

数学 中2 74 平行四辺形になる条件 Youtube
Math 平行四辺形 平行四辺形になることの証明 働きアリ

Math 平行四辺形 平行四辺形になることの証明 働きアリ
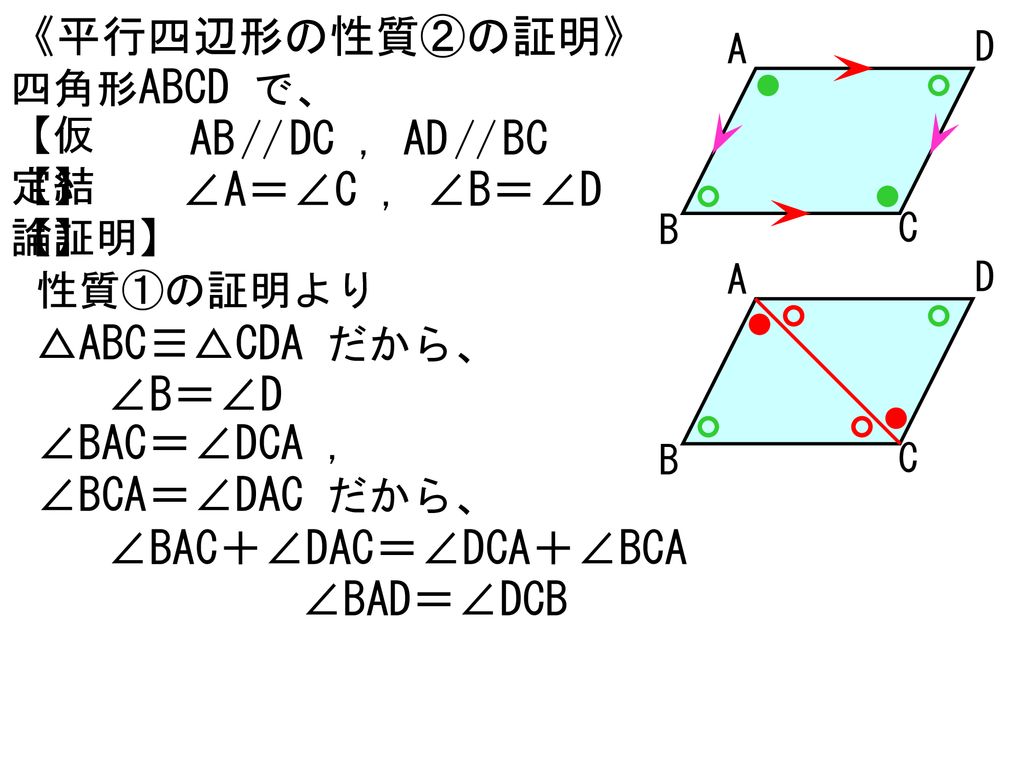
5 図形と合同 2章 平行四辺形 1 平行四辺形 5時間 Ppt Download
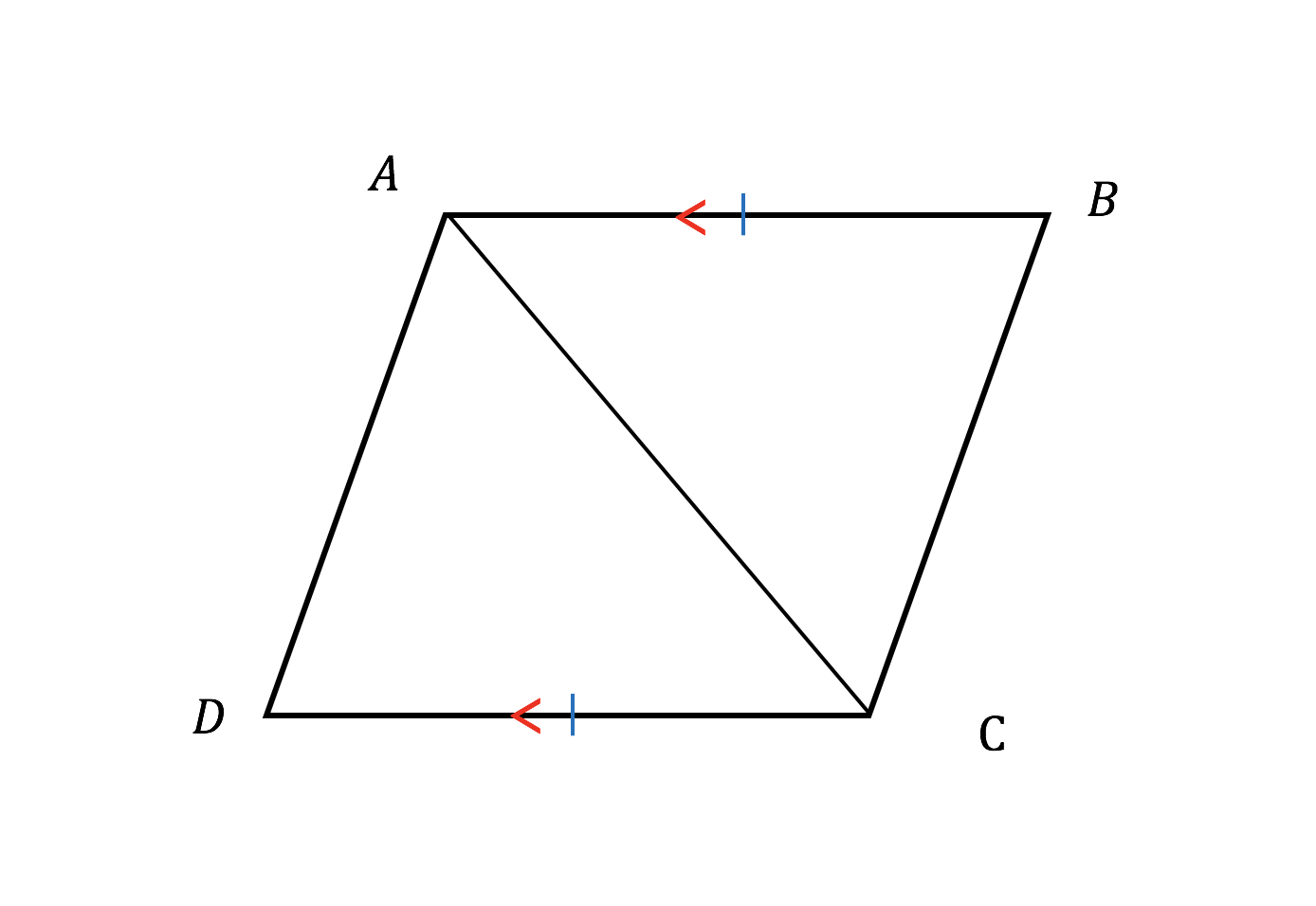
3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ
2

中2数学 平行四辺形の証明 練習編 映像授業のtry It トライイット
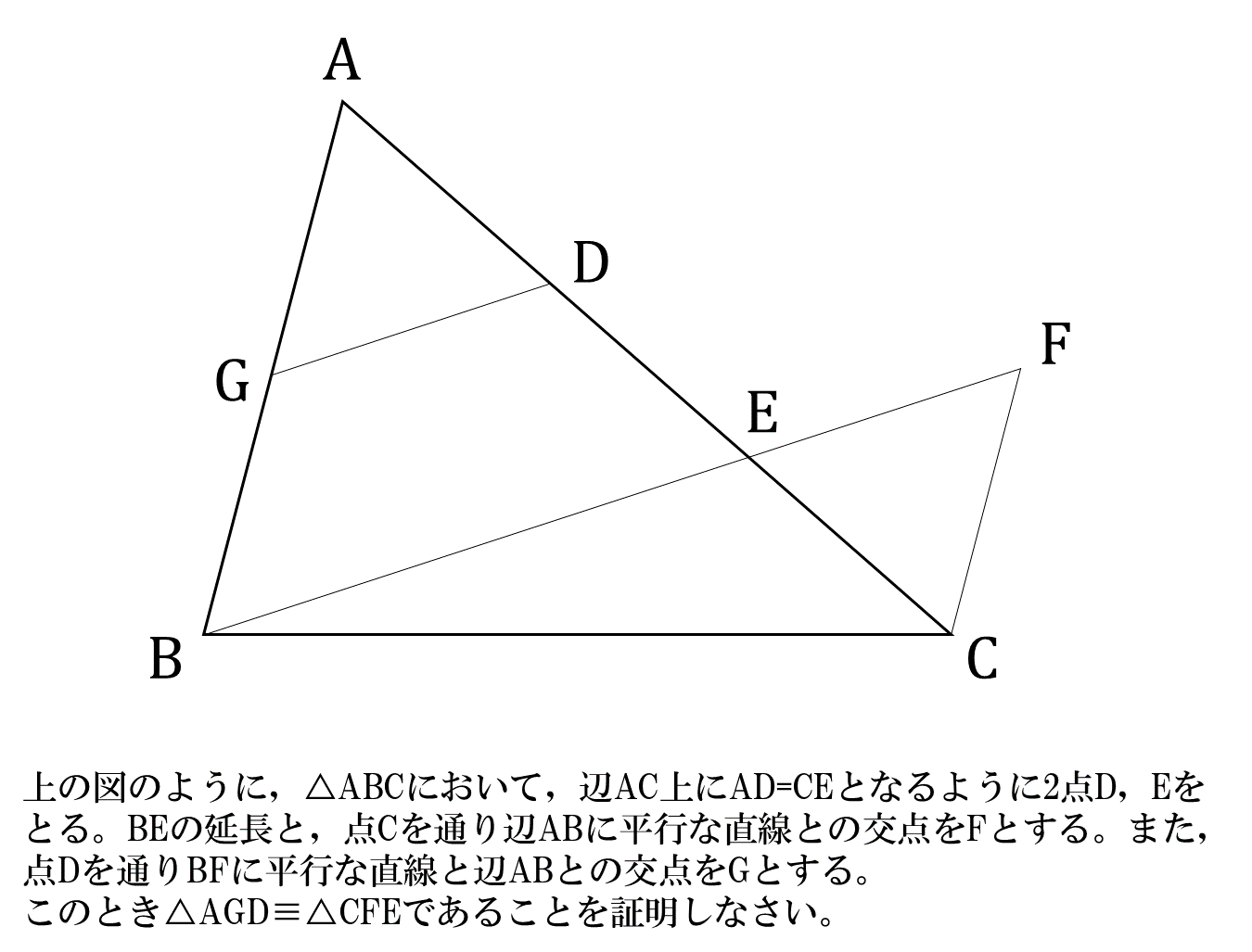
数学 中学証明問題を解く4つのポイント
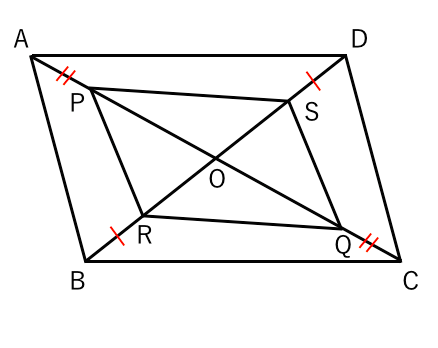
平行四辺形abcdで対角線bd上に Be Dfとなる点をとった 四 Yahoo 知恵袋
平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典

中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット

ベクトルの外積と平行四辺形の面積 身勝手な主張
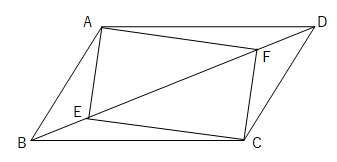
中2数学 平行四辺形の証明のポイントと練習問題 Examee
数学bの問題なんですが平行四辺形abcdでab Adのときac D Yahoo 知恵袋
Search Q B9 E5 B9 E8 A1 8c E5 9b 9b E8 Be Ba E5 Tbm Isch
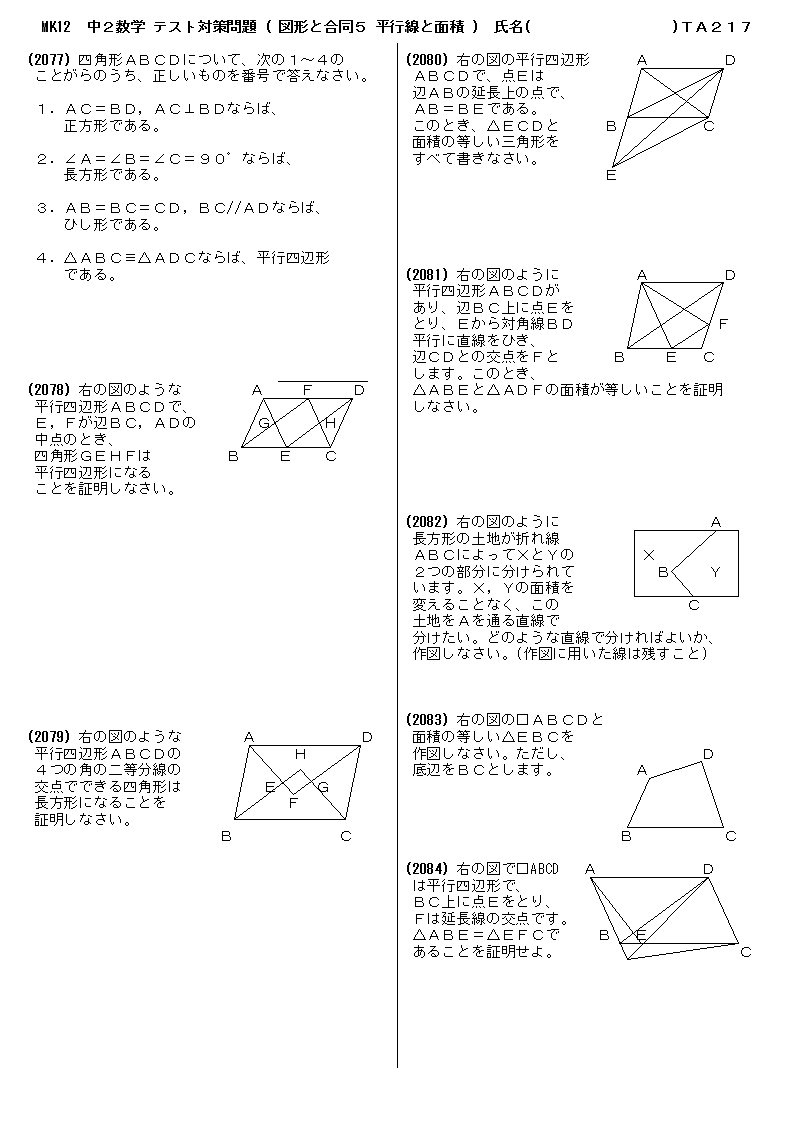
平行 四辺 形 の 証明 平行四辺形の証明 ズバリ解き方はこれ 中学生 数学 公式 家庭教師のアルファ
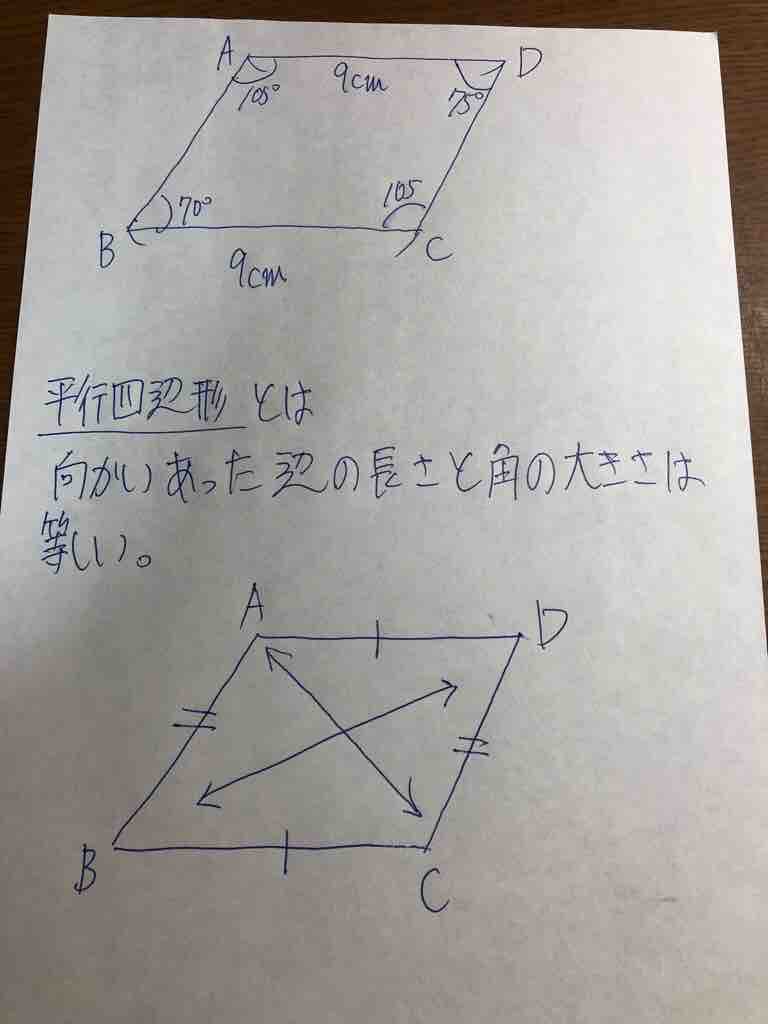
平行四辺形 数学の記録
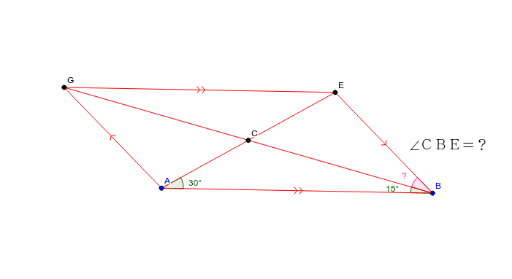
難問に挑戦しよう Geogebra
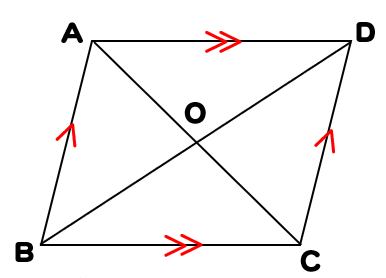
平行四辺形の定義と性質 証明問題の解き方 数学fun
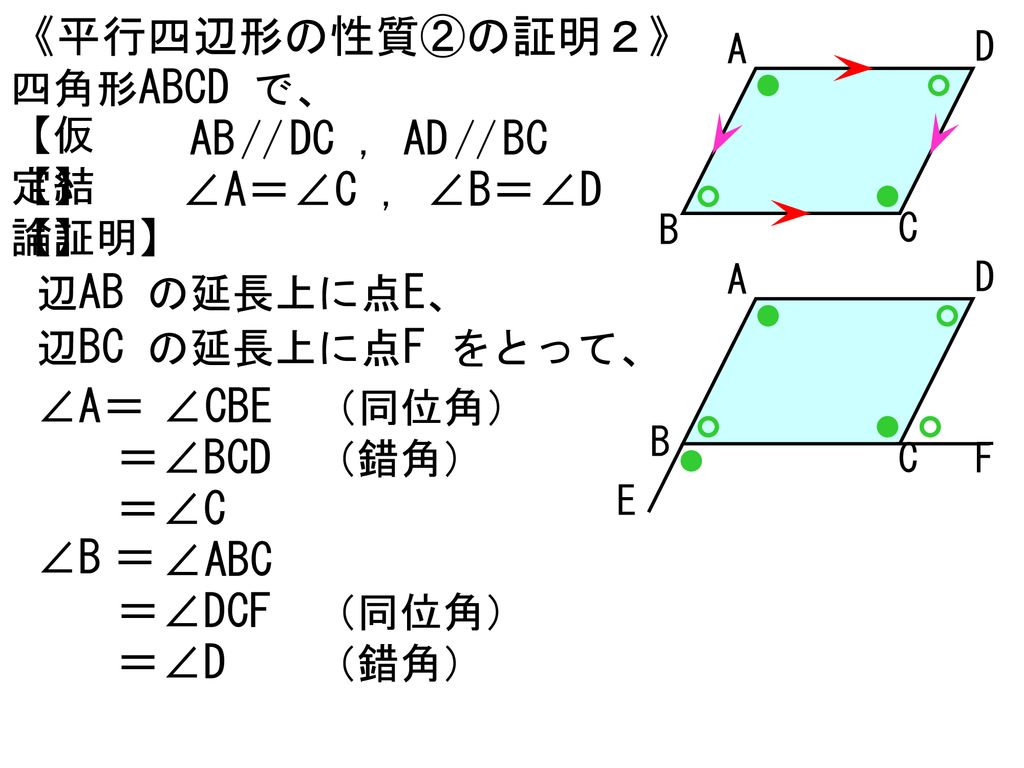
5 図形と合同 2章 平行四辺形 1 平行四辺形 5時間 Ppt Download
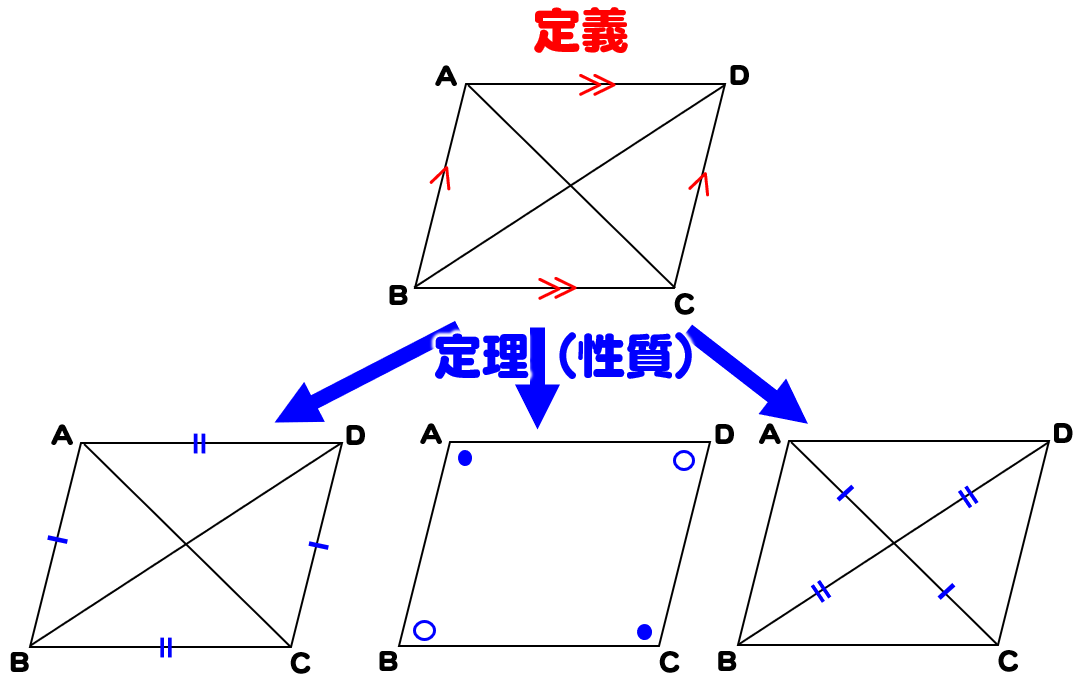
平行四辺形の定義と性質 証明問題の解き方 数学fun

平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ

平行四辺形になるための条件 勉強 Youtube スタディチューブ
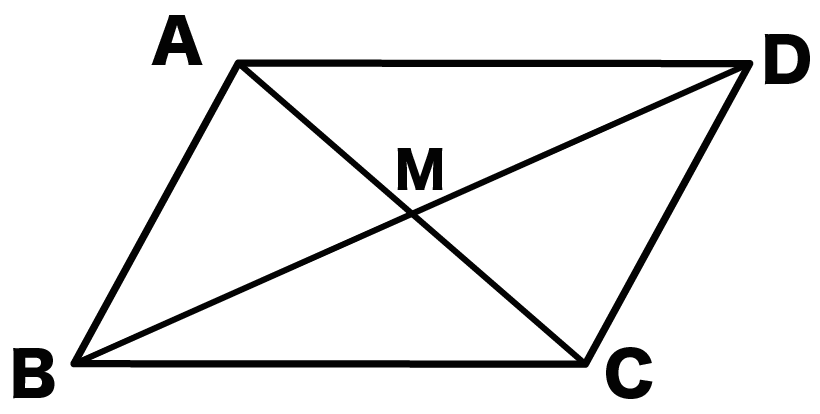
中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく
壮大 特別 な 平行 四辺 形 壁紙 配布

中2 数学 証明 数学 算数のq A 解決済み Okwave

平行四辺形の面積の求め方 公式と計算例

平行四辺形の証明と角度を求める問題の解き方 現役塾講師のわかりやすい中学数学の解き方
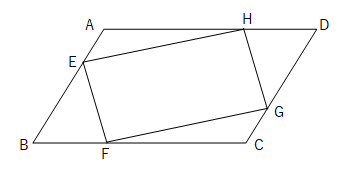
中2数学 平行四辺形の証明のポイントと練習問題 Examee

この証明の問題の 4 がわかりません Clear

平行四辺形の対角線はそれぞれの中点で交わることの証明 をしないとい 中学校 教えて Goo
図のように 平行四辺形abcdの頂点aから辺bc Cdにひいた垂線とそれぞれの辺 Yahoo 知恵袋
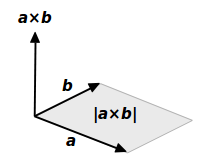
ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門
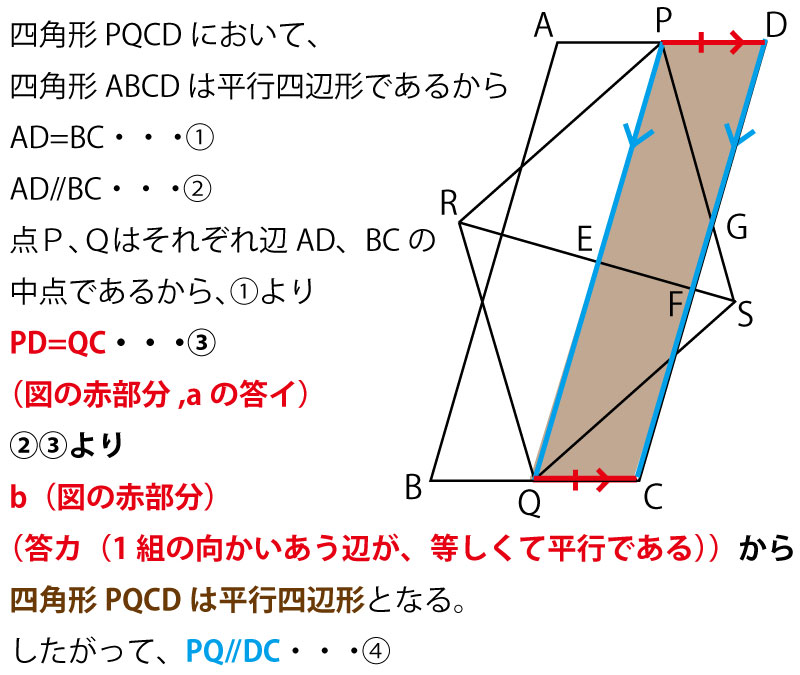
19年前期 千葉県公立高校入試 数学 第4問 図形の証明 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ

中学数学 平行四辺形になることの証明 その3 中学数学の無料オンライン学習サイトchu Su

今 平行四辺形の証明問題をしています 授業のスピードが早く 中学数学に関する質問 勉強質問サイト

平行四辺形の3つの性質 数学教材

平行四辺形の面積の求め方 公式と計算例
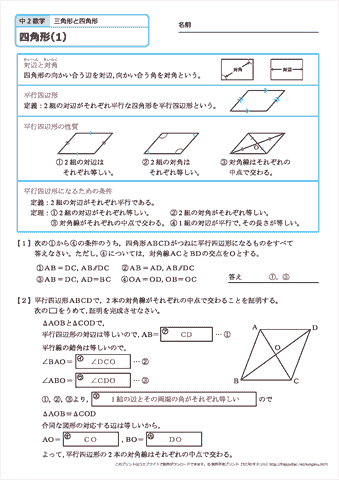
中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ

平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
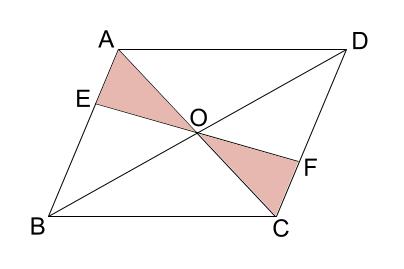
中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su

中学数学 平行四辺形の証明問題を徹底解説 数スタ
右の図のように 平行四辺形abcdを対角線bdを折り目として折り返し Yahoo 知恵袋
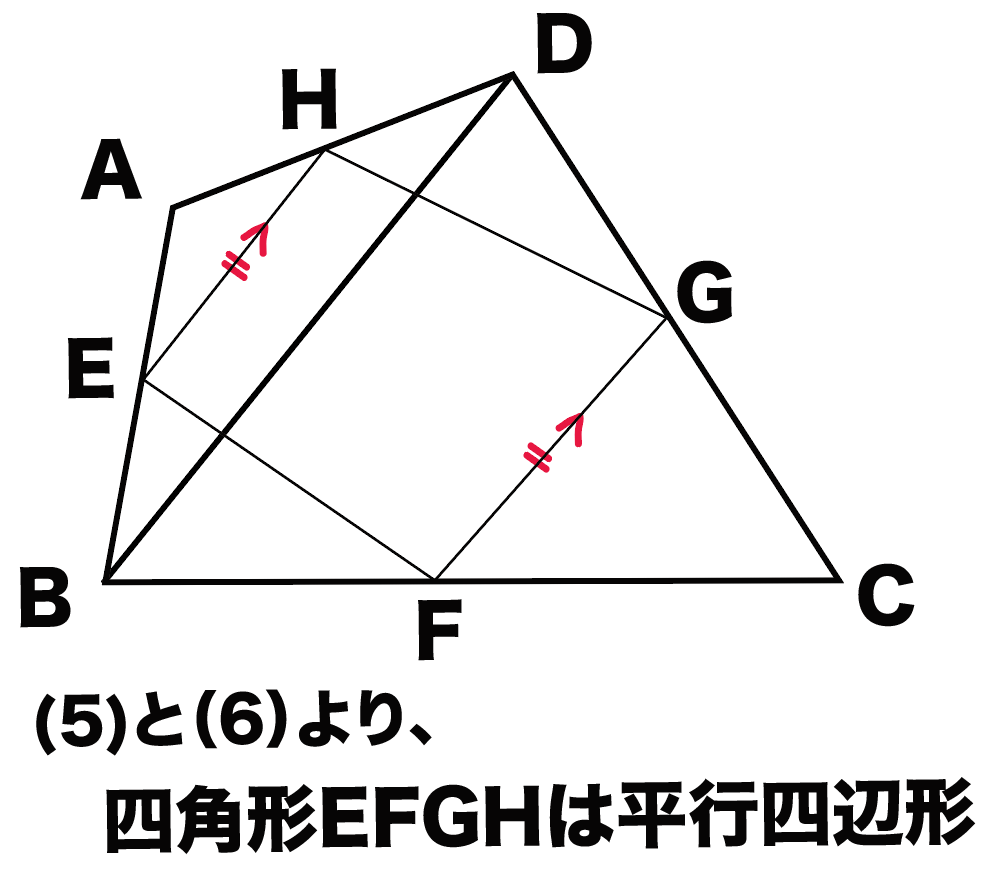
中点連結定理 平行四辺形の証明問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
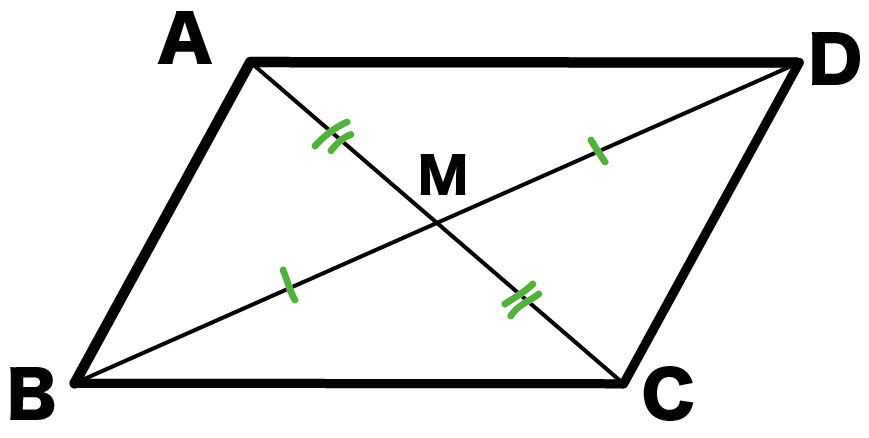
中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく
特別な平行四辺形2
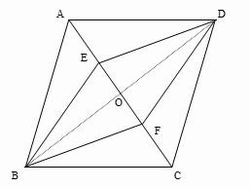
入試対策 図形の証明問題3問 いろいろな解き方を考えてみよう 駿英式 勉強術
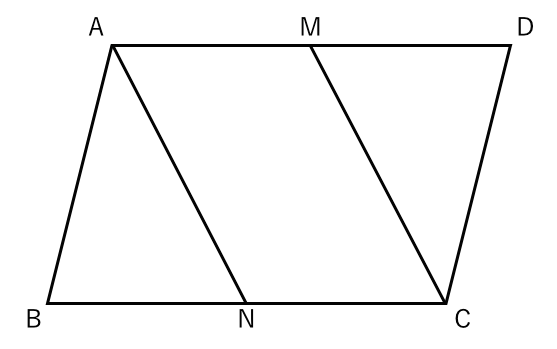
平行 四辺 形 の 性質 平行四辺形の性質1
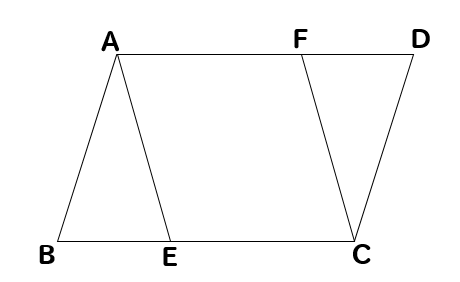
中学数学 平行四辺形の証明問題を徹底解説 数スタ

中2数学 平行四辺形の証明 練習編 映像授業のtry It トライイット
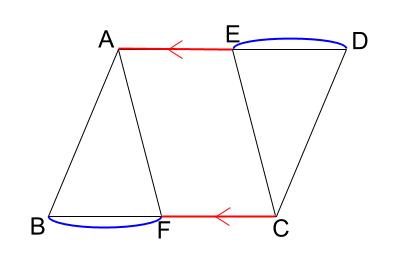
中学数学 平行四辺形になることの証明 その1 中学数学の無料オンライン学習サイトchu Su

中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット

対角が等しいことを証明するとは思います 具体的な証明の方法を 中学数学に関する質問 勉強質問サイト

平行四辺形の対角線はそれぞれ中点で 高校数学に関する質問 勉強質問サイト

中2 数学 四角形4 平行四辺形の証明2 17分 Youtube

Math 平行四辺形 平行四辺形になることの証明 働きアリ

平行四辺形abcdの対角線をo Bp Pc 1 2となるpと 中学数学に関する質問 勉強質問サイト

ベクトルの外積と平行四辺形の面積 身勝手な主張
平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典

証明の仕方を教えてください Clear
中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su
平行四辺形の証明と角度を求める問題の解き方 現役塾講師のわかりやすい中学数学の解き方
中点連結定理 平行四辺形の証明問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
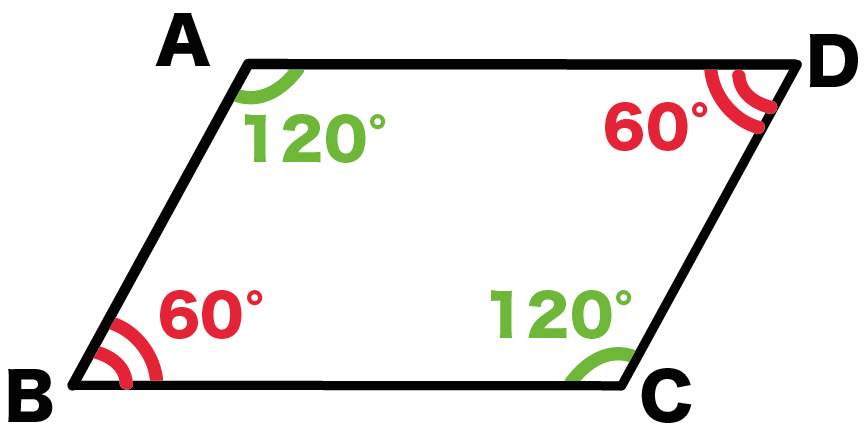
中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく
平行四辺形の性質の利用2

平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を抑えよう 遊ぶ数学

関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ
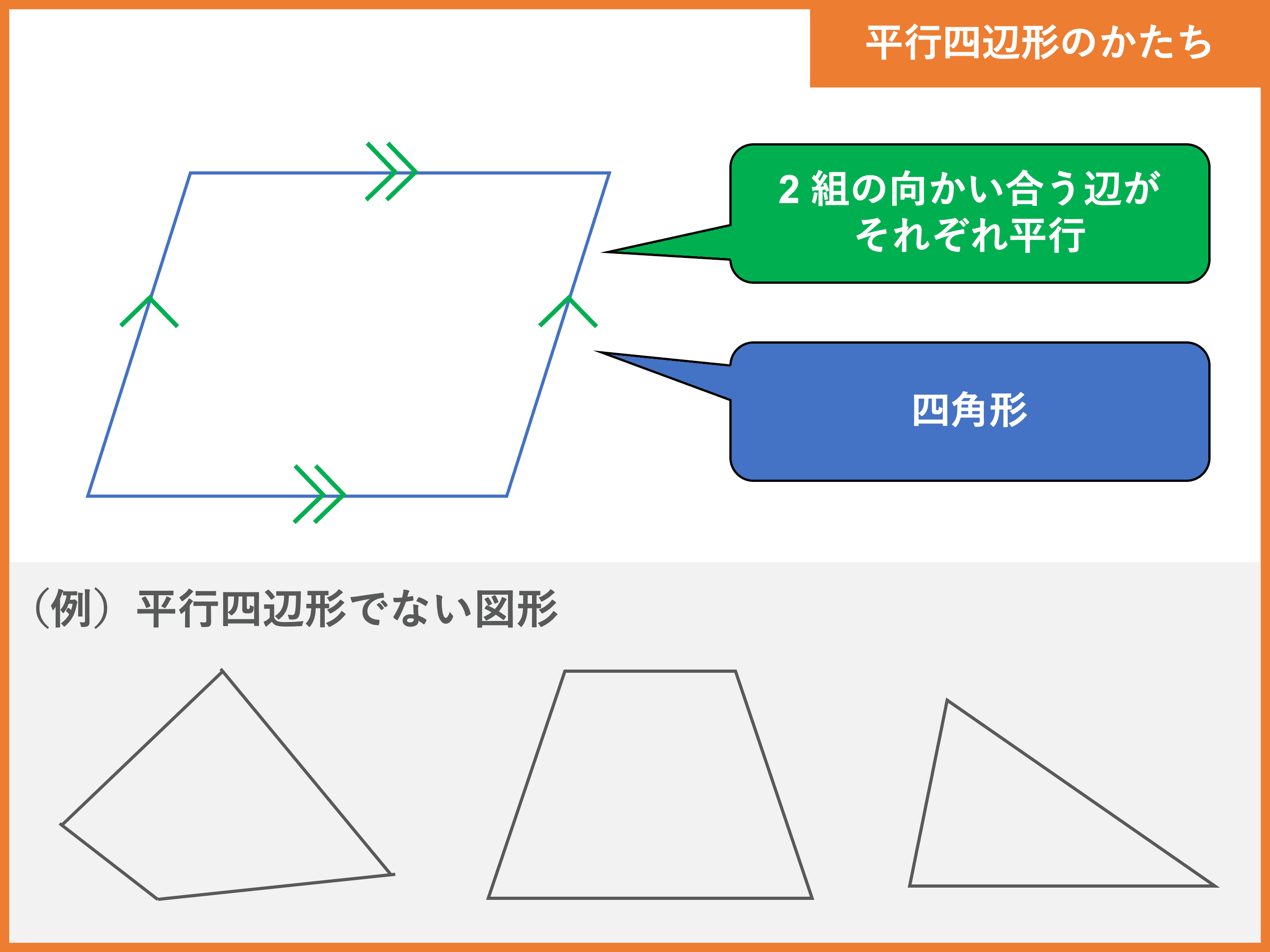
平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
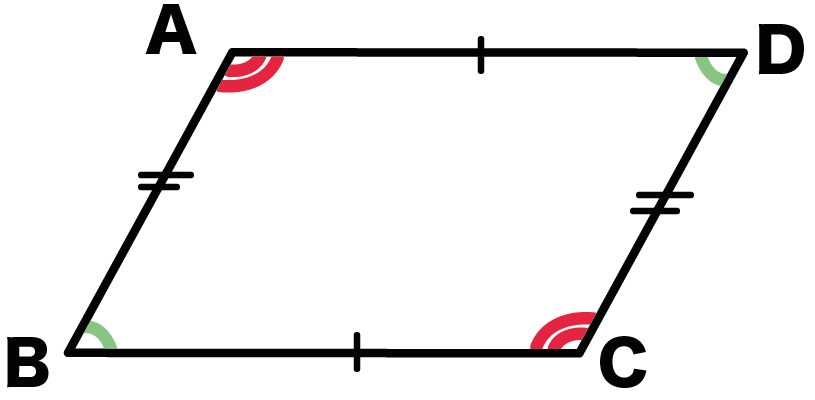
中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく
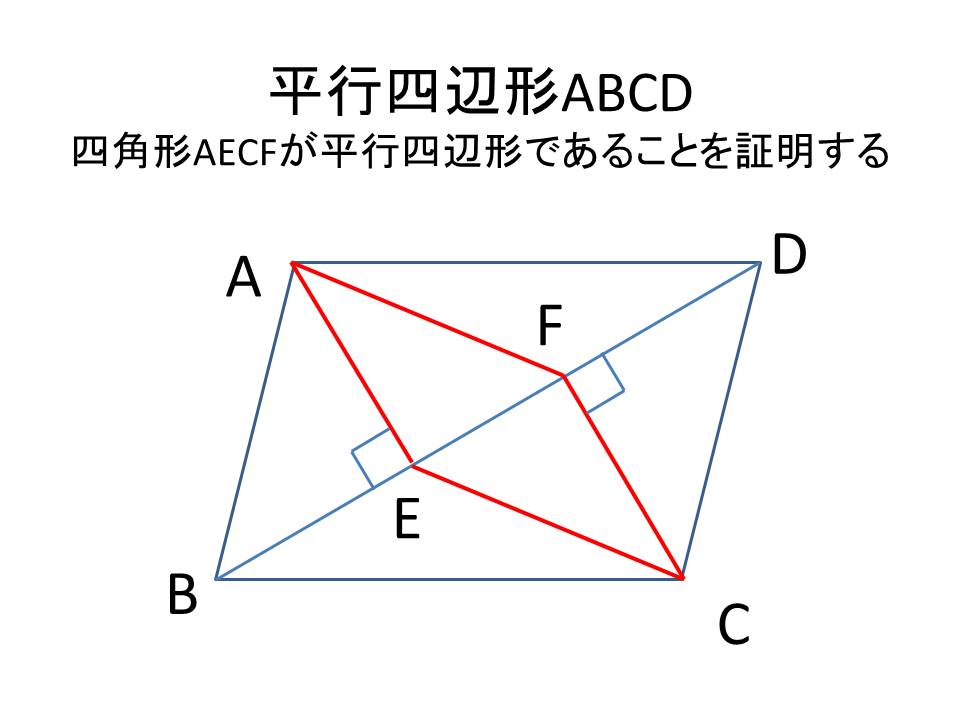
中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ

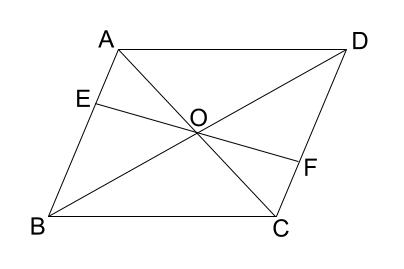
平行四辺形abcdの対角線の交点をoとして 対角線bdにoe ofとなる2 中学校 教えて Goo

高校数学b ベクトルの成分表示と平行四辺形 受験の月
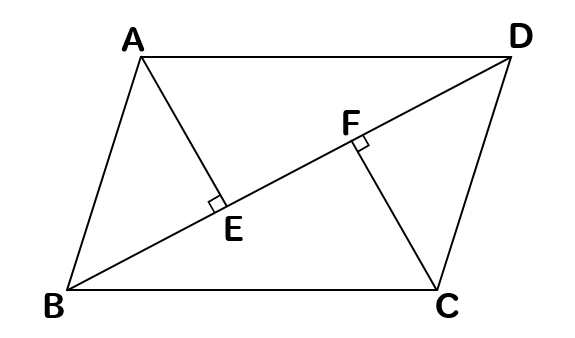
中学数学 平行四辺形の証明問題を徹底解説 数スタ

平行四辺形の面積の求め方 公式と計算例

数学 中学数学に関する質問 勉強質問サイト
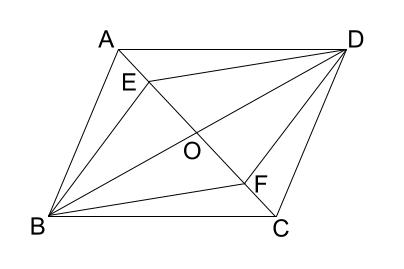
中学数学 平行四辺形になることの証明 その1 中学数学の無料オンライン学習サイトchu Su

平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を抑えよう 遊ぶ数学
平行四辺形の性質の利用2
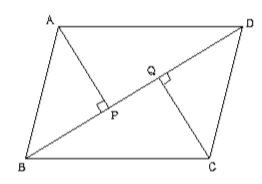
中2数学 平行四辺形の証明のポイントと練習問題 Examee

平行四辺形の定義と性質 証明問題の解き方 数学fun
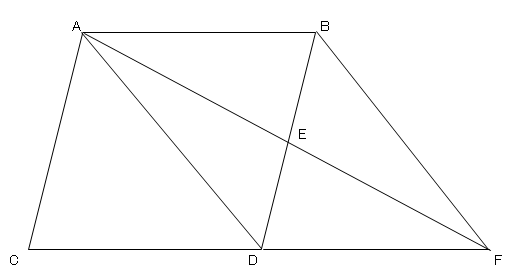
年の最高 平行 四辺 形 問題 Trendeideas5

平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ

この証明の解き方教えて欲しいです Clear

平行四辺形になるための条件 数学教材

平行四辺形と証明 Youtube

平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方 現役塾講師のわかりやすい中学数学の解き方
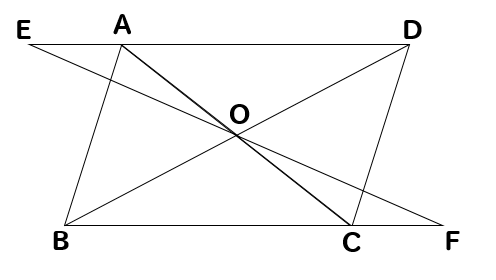
中学数学 平行四辺形の証明問題を徹底解説 数スタ

平行四辺形abcdの頂点a Cから対角線bdに垂線を引き 対角線との交点をそれぞれ Clear

中2数学 平行四辺形の証明 授業ノート 中学生 数学のノート Clear
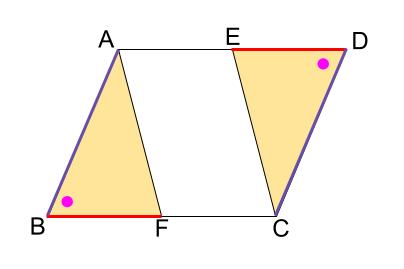
中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su




