ピタゴラス の 定理 の 証明
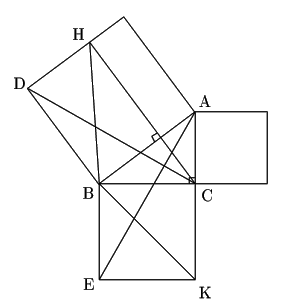
この定理には数百通りもの異なる証明が知られている。ここにいくつかの代表的な証明を挙げる。 以下では頂点 a, b, c からなる三角形を abc と表す。.
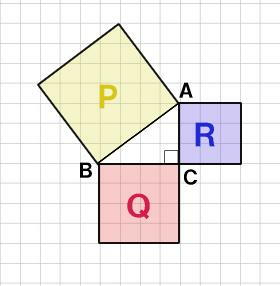
ピタゴラス の 定理 の 証明. このピタゴラス数の性質を使うと、フェルマーの最終定理のn=4の場合の証明をすることができます。 では、 フェルマー 自身が余白に書き残してくれていた、証明の中身を見ていきましょう。. 三平方の定理には数百もの証明方法があります。その中でも、ユークリッドが主著『原論』の中で紹介した、幾何的な証明について説明します。 Ⅰ 三平方の定理とは Ⅱ ユークリッドの証明 Ⅲ その他の証明方法. ピタゴラス数のある性質 自然数 a、b、c が、a 2 +b 2 =c 2 を満たすとき、ピタゴラス数といわれる。 このような a、b、c は、 a=m 2 -n 2 、 b=2mn 、 c=m 2 +n 2 と書かれる。 ただし、m、n は、互いに素な自然数で、どちらかは偶数、かつ、m>n とする。.
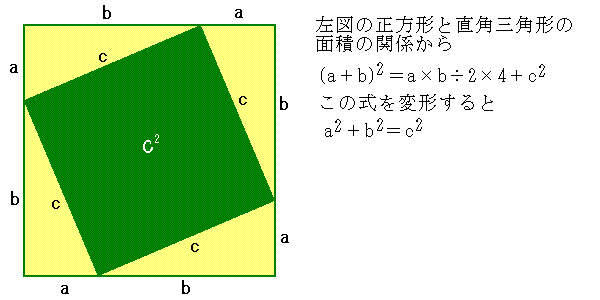
「ピタゴラスの定理」を用いれば、 整数でも分数でもない「無理数」が出てくるときもある。 1 2 + 1 2 = Z 2 Z = √2 (無理数) この整数でも分数でもない「無理数」という存在があることを 弟子の一人が「ピタゴラスの定理」を使って、証明してしまったから. A 2 + b 2 = c 2 ⊿ 直角三角形で、それぞれの辺の長さを 2 乗した正方形を考えます。 その三つの正方形の面積の関係性を語ったのが《三平方》の定理です。 底辺 2 + 高さ 2 = 斜辺 2. ピタゴラスは、この定理を証明したそうですね。 ところで、彼はこの定理を発見したのでしょうか? あるいは、発明(創造)したのでしょうか? {発見したのであれば、この定理がこの世に既にあった(実在していた)のだし.
ピタゴラスの定理 ピタゴラスの定理の証明 この定理には数百通りもの異なる証明が知られている。ここにいくつかの代表的な証明を挙げる。以下では頂点 a, b, c からなる三角形を abc と表す。また、各辺 ab, bc. ピタゴラスの定理を証明したものである」 とのみ記されている。 この図からどのようにして三平方の定理が 導き出されるのだろうか。 ウモクホ数学に匹敵する学問体系を築き上げた 古代中国の学者に思いをはせながら、 証明方沵を考えてみてください。. 目次ピタゴラスの定理、ピタゴラス方程式原始ピタゴラス数とは何かピタゴラス数の分類偶数、奇数。いくつか性質の証明原始ピタゴラス数を作り出す公式一番親しまれてきた方程式 ピタゴラスの定理、ピタゴラス方程式 直角三角形に関し.
森下, 四郎 『ピタゴラスの定理100の証明法 幾何の散歩道』 プレアデス出版、06年1月。isbn 4-7687-0879-x。 — 発売:現代数学社。 森下, 四郎 『ピタゴラスの定理100の証明法 幾何の散歩道』 プレアデス出版、10年8月、改訂版。isbn 978-4--36-0。. 中学生でもわかる三平方の定理(ピタゴラスの定理)の証明って??こんにちは!Dr.リードだぞいっ。 今回のテーマは三平方の定理(ピタゴラスの定理)だ。聞いたことあるかな? 紀元前572年ごろのギリシア人のピタゴラスさんが発見したから. 森下四郎『ピタゴラスの定理100の証明法 幾何の散歩道』プレアデス出版、10年8月、改訂版。 isbn 978-4--36-0。 森下四郎『ピタゴラスの定理をめぐる2つの謎 三平方の定理の謎』プレアデス出版、10年12月。 isbn 978-4--39-1。 関連項目.
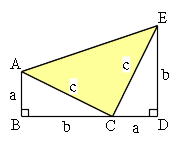
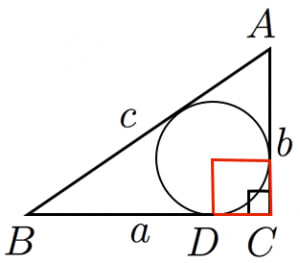
逆ピタゴラスの定理を使えば, 命題1 を図形的に示すことができます。 まず,斜辺を ,残りの2辺を , となる直角三角形を用意します( , , はピタゴラス数)。このとき,斜辺からの三角形の高さを とすると,逆ピタゴラス数の定理より ,すなわち と. ピタゴラスの定理の一つの証明法(原 憲昭) rarc rr kanc >&13>' ― 2 ― ah が接角を2直角に等しくする。 それゆえΓa は ah と一直線をなす。 同じ理由で ba もaΘと一 直線をなす。そして角ΔbΓは角zba に,共に直 角であるがゆえに等しいから,双方に角 abΓが 加えられたとせよ。. ピタゴラスの定理の証明法は数多く知られていますが, そのうちの一例を示します。下図のような正方形を考えます。つまり, 一辺の長さは matha + b/math です。.
三平方の定理でおなじみの、天才数学者・ピタゴラス。世界最古の数学者ともいわれているピタゴラスは、数学者の中でもかなりの変人だったそうです!今回は、天才数学者ピタゴラスの変人エピソードをご紹介します。 Contents0.1 目次1 天才数学. ^大矢, 真一『ピタゴラスの定理』東海大学出版会〈Tokai library〉、01年8月。ISBN 4-486--4。 ^ 大矢, 真一『ピタゴラスの定理』東海大学出版会〈東海科学選書〉、1975年。 ^ 大矢, 真一『ピタゴラスの定理』東海書房、1952年。 ^ 亀井喜久男. この記事ではこんなことを書いています 三平方の定理(ピタゴラスの定理)には多くの証明方法がありますが、ここでは円を利用した証明を紹介しましょう。 図形を描いて、その長さを調べていくだけで三平方の定理が証明できてしまう面白い証明方法です。 三平方の定理の簡単な復習 三平.
ピタゴラスの定理 大矢真一著 (Tokai library) 東海大学出版会, 01.8. 定理原始的なピタゴラス数においては、次が成り立つ。 z≡1 (mod 4) 証明z=m 2 +n 2 において、mとnは偶奇性が異なるから、m=2k,n=2k'+1(k,k'は整数)とおける。. 三平方の定理には数百もの証明方法があります。その中でも最も基本的で歴史の古い、ピタゴラスが考えた証明について説明します。 ①三平方の定理とは ②ピタゴラスの証明 ③その他の証明方法へ ①三平方の定理.
森下, 四郎 『ピタゴラスの定理100の証明法 幾何の散歩道』 プレアデス出版、10年8月、改訂版。isbn 978-4--36-0。 森下, 四郎 『ピタゴラスの定理をめぐる2つの謎 三平方の定理の謎』 プレアデス出版、10年12月。isbn 978-4--39-1。 関連項目. ピタゴラスの定理の証明を集めた本は多数あるが,今回の記事を書くにあたり,『ピタゴラスの定理 $100$ の証明法 ― 幾何の散歩道』(森下四郎著,プレアデス出版)を参考にした.証明が種類別に分けられ,系統的に説明されていて分かりやすい.考えて.

ピタゴラスの定理 Lien と W4

ピタゴラスの定理
ピタゴラスの定理 ウソの国ー詩と宗教 戸田聡 St5402jp
ピタゴラス の 定理 の 証明 のギャラリー
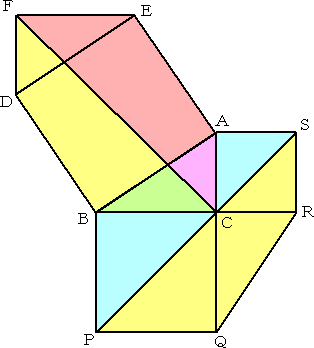
ピタゴラスの定理とその証明
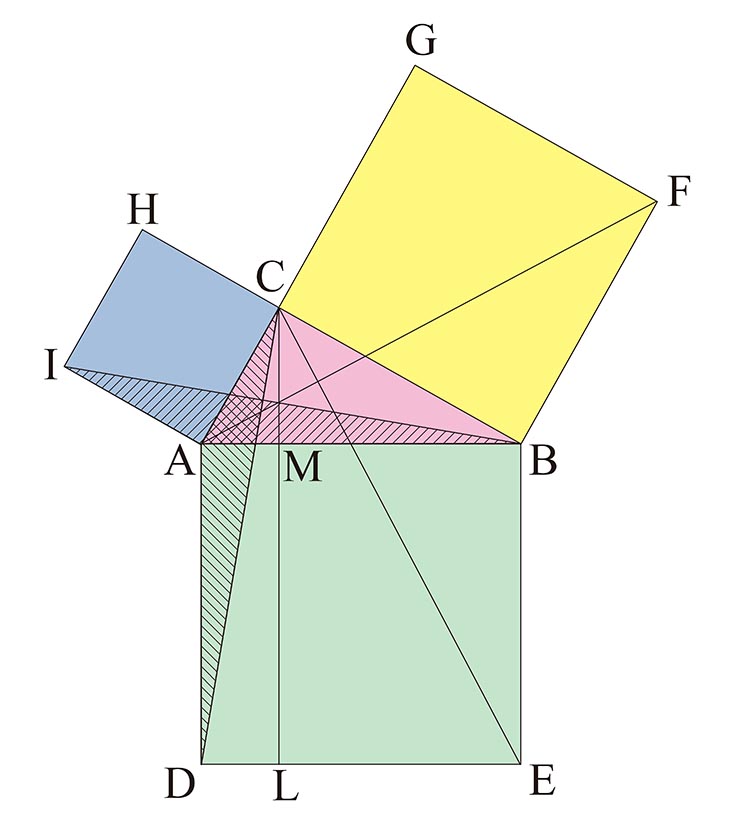
コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション

Amazon Co Jp ピタゴラスの定理 100の証明法 幾何の散歩道 森下 四郎 本

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

中学数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube

三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導
三平方の定理

そらいあんぐる ピタゴラスの三平方の定理 B2 C2 構成三角形で証明を ピタゴラス 三角形 あん
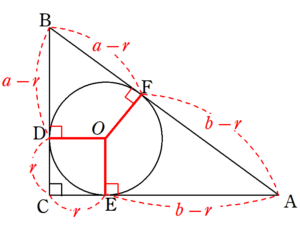
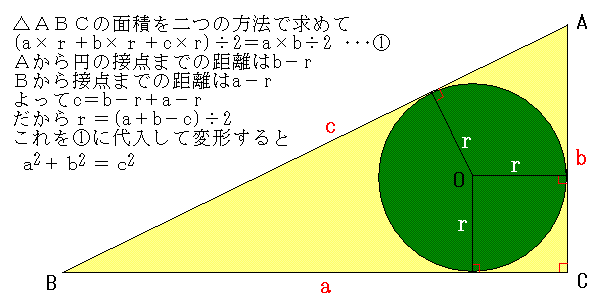
三平方の定理の証明 内接円の利用 Fukusukeの数学めも

ピタゴラスの定理とその証明

中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook
Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ
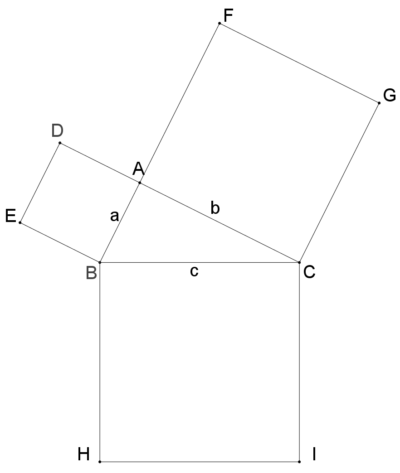
三平方の定理の証明 ユークリッドの証明 Fukusukeの数学めも
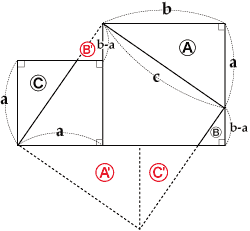
コラム ピタゴラスの定理 江戸の数学

ねこ騙し数学
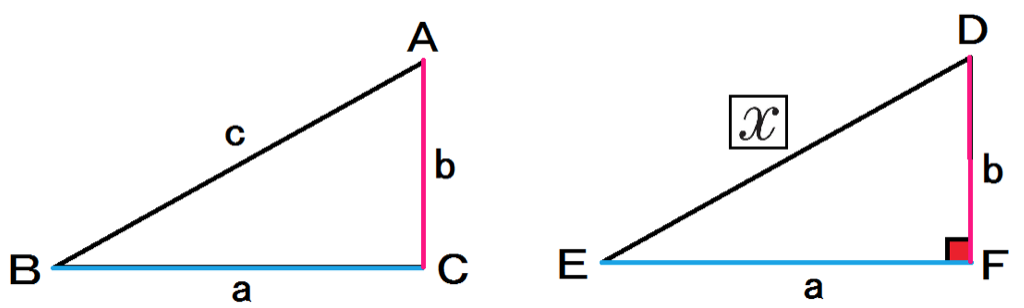
中3数学 2分でわかる 三平方の定理の逆 Qikeru 学びを楽しくわかりやすく
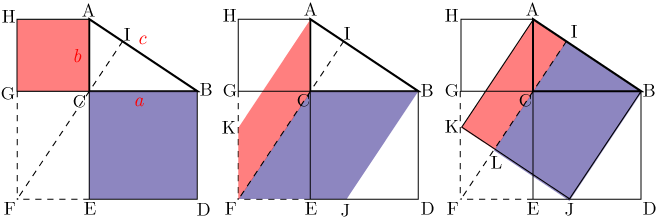
三平方の定理 ピタゴラスの定理
感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
ピタゴラスの定理の拡張のしかた

中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

中学数学 三平方の定理
ピタゴラスの定理 の別証明集
三平方の定理
三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
ピタゴラスの定理の簡単な証明方法ありますか Quora
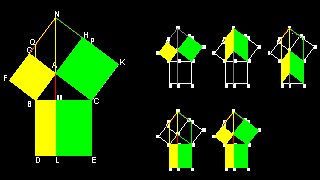
Many Proofs Of Pythagorean Theorem
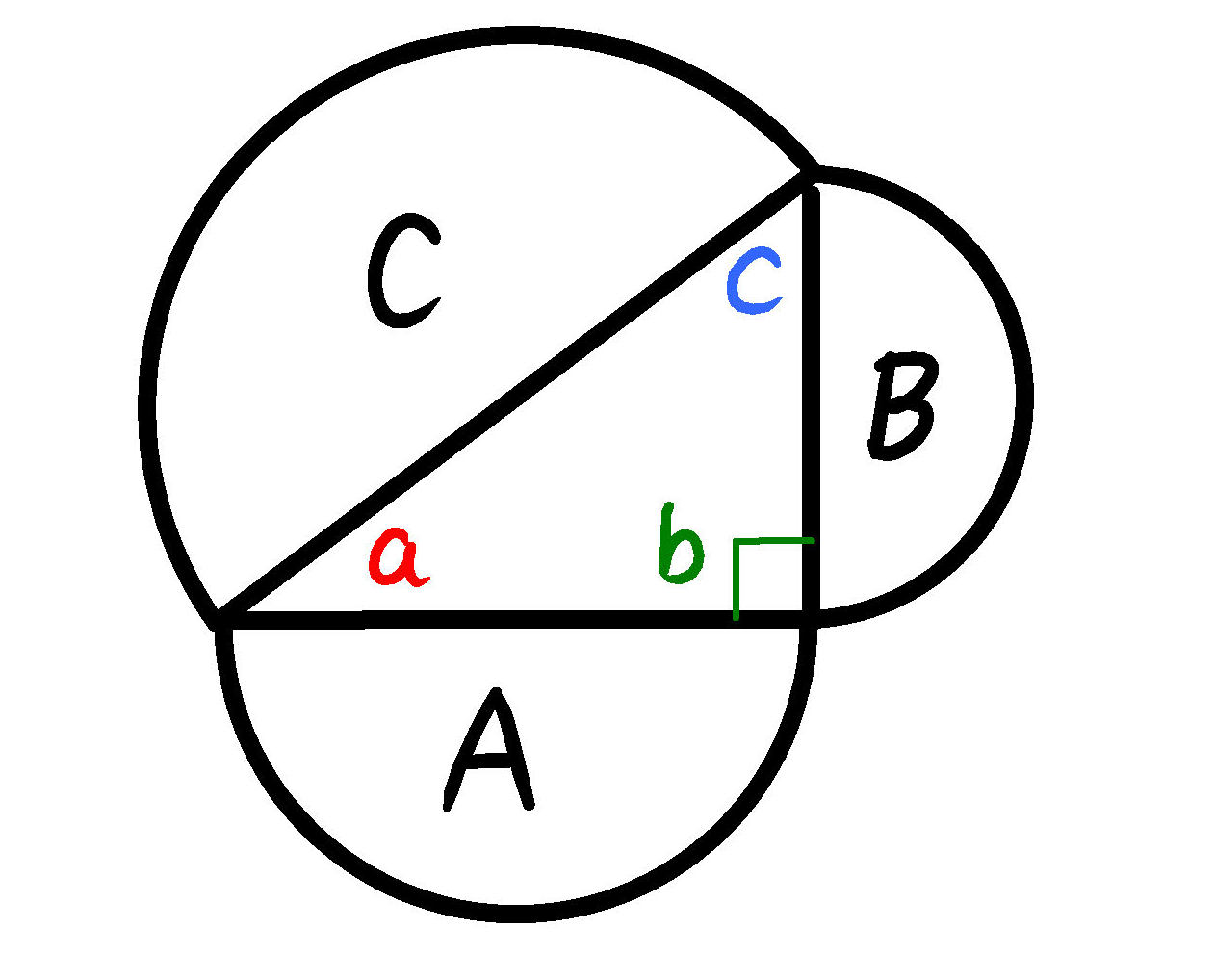
ピタゴラスの定理の証明 大栗博司のブログ

ピタゴラスの定理 の証明アニメ2 ピタゴラス自身による証明 Youtube

ピタゴラスの定理 の証明アニメ6 ユークリッド Youtube
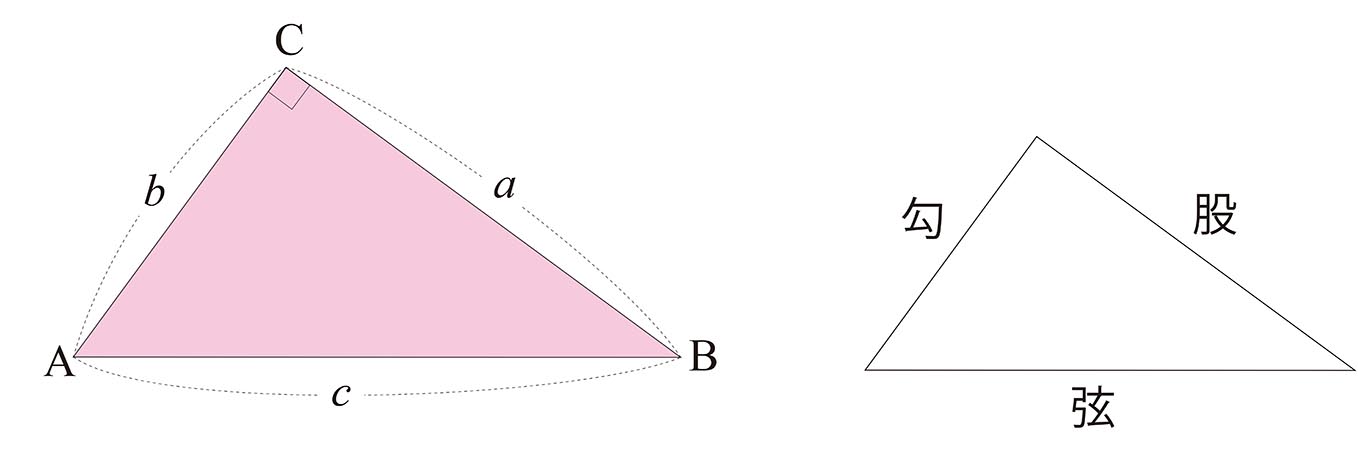
コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション

三平方の定理の証明と使い方

必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ
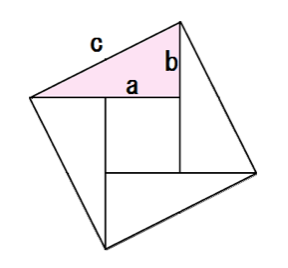
中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく
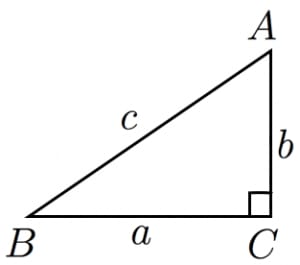
三平方の定理の4通りの美しい証明 高校数学の美しい物語

三平方の定理の証明 直感的に分かる図で解説します 数学fun

カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4
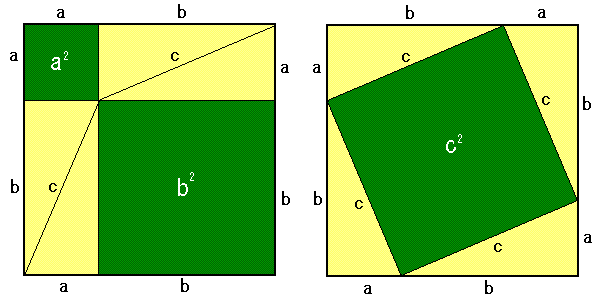
三平方の定理の4通りの美しい証明 高校数学の美しい物語

必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ
三平方の定理

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

ピタゴラスの定理 ピタゴラスの定理の証明 Weblio辞書

ピタゴラスの定理 の証明アニメ4 バスカラ Youtube

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく
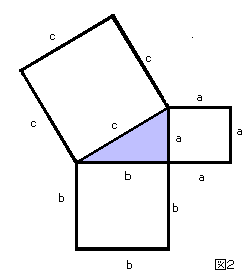
ピタゴラスの定理が証明できた

ピタゴラスの定理 Security Akademeia
三平方の定理
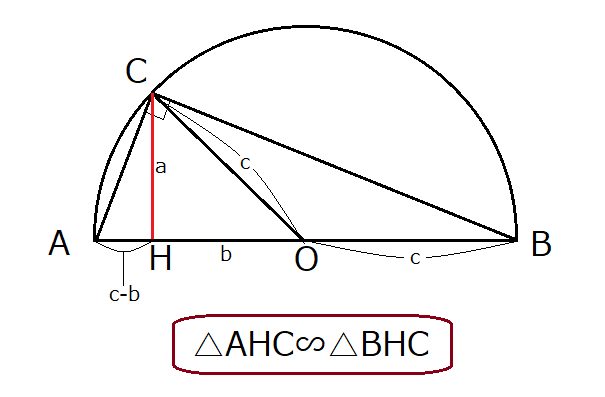
三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋
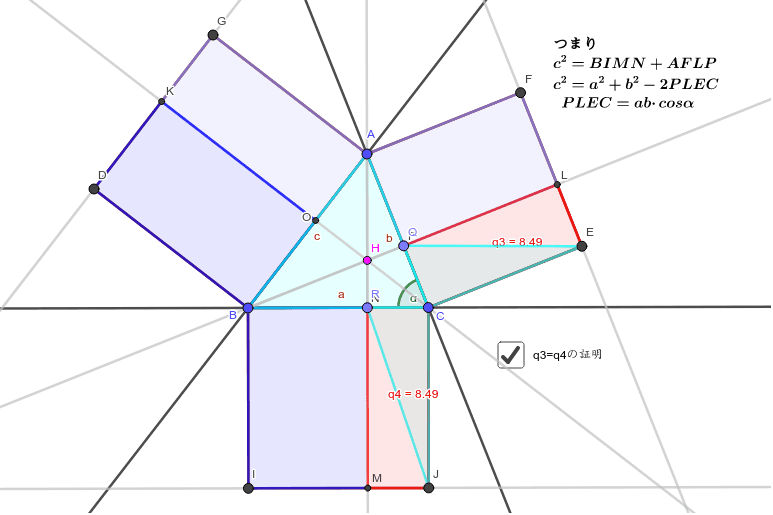
ピタゴラスの定理 ユークリッドの証明 Geogebra

必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ

三平方の定理の証明と使い方
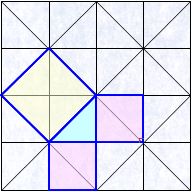
見えますか タイルの模様からピタゴラスの定理 Note Board

三平方の定理
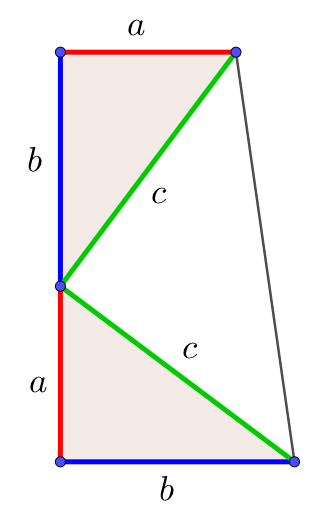
三平方の定理の証明3 大統領の台形 キソカラ

ピタゴラスの定理 Wikipedia
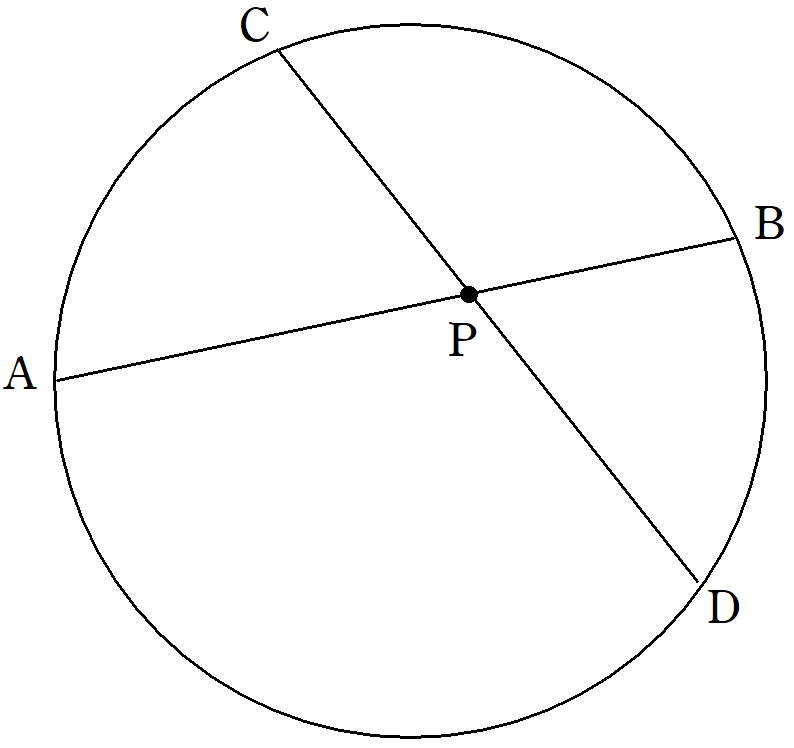
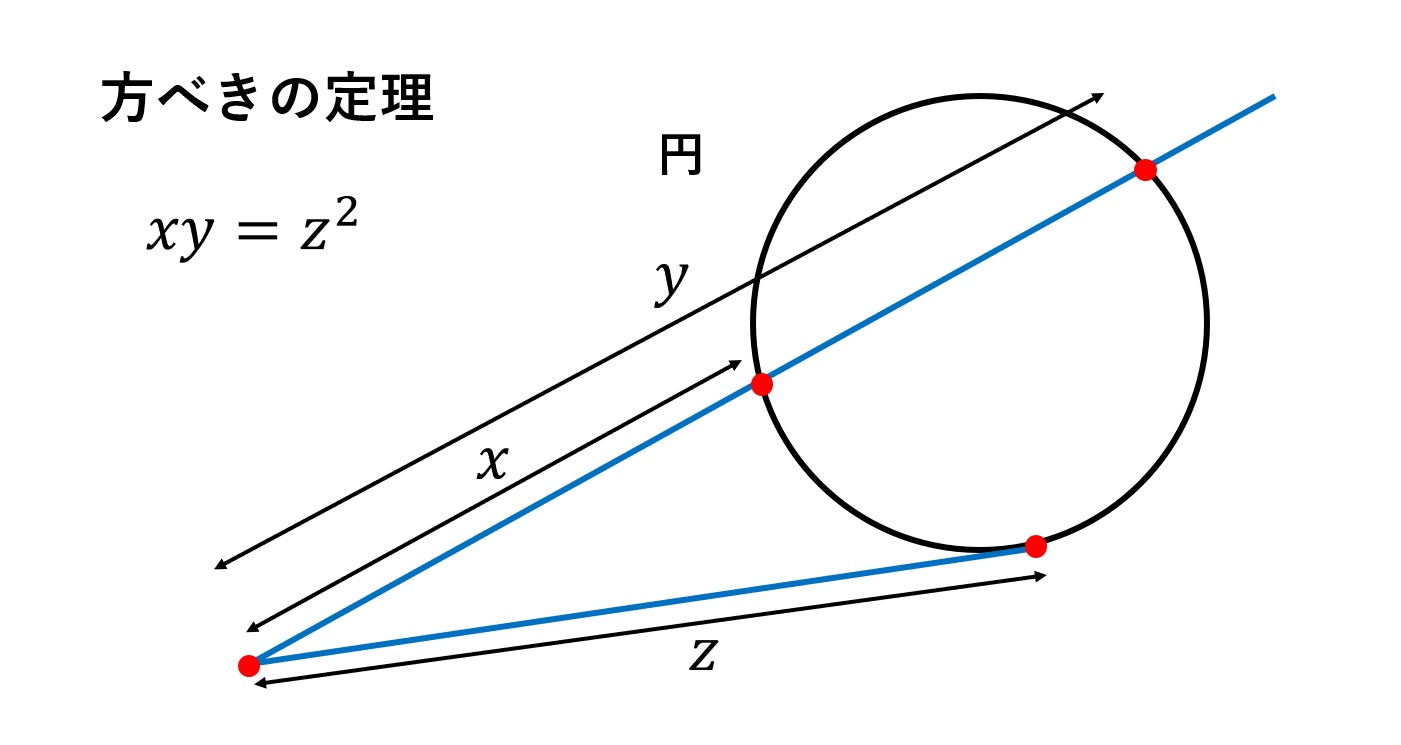
三平方の定理の証明 方べきの定理の利用1 Fukusukeの数学めも
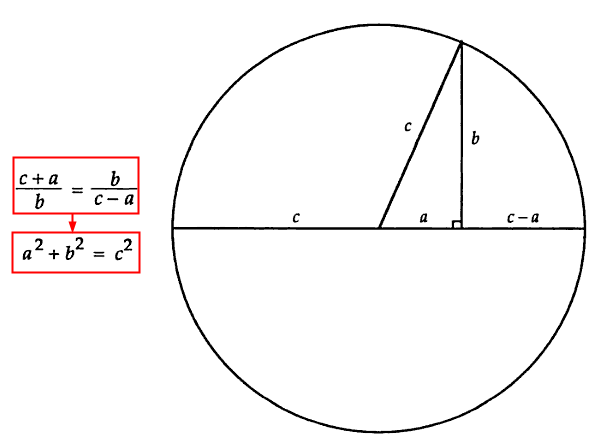
数学の概念 を視覚的かつ美しく表現したグラフィックいろいろ Gigazine

三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張

三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張
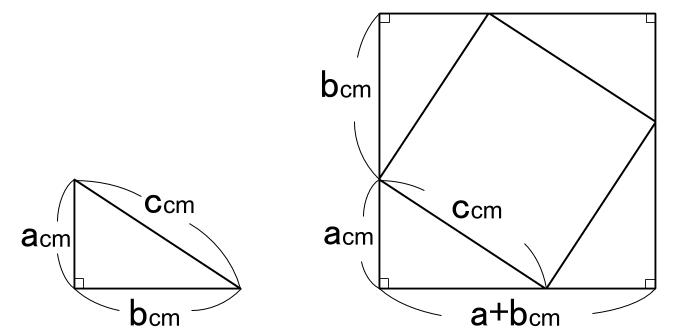
中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su
Q Tbn 3aand9gcqmzvxdxyji6npy6kxznl41rwywayls3hdrtb Rhvzquu Xi5vi Usqp Cau

正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
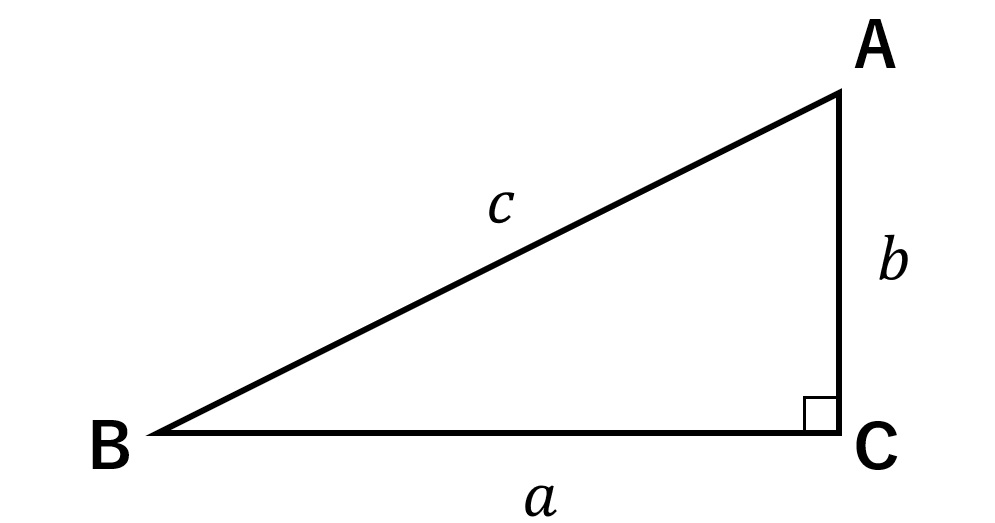
感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
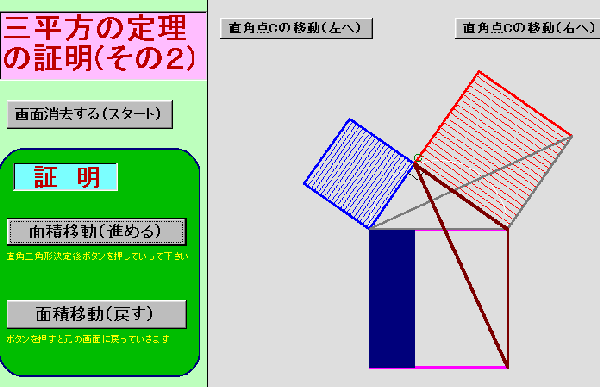
三平方の定理

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

コラム ピタゴラスの定理 江戸の数学
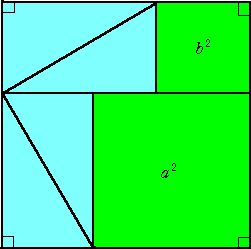
ピタゴラスの定理とその証明

Q Tbn 3aand9gcqbfxommah9nzhmif2vzhsb 1cupdedhpy7hq Usqp Cau
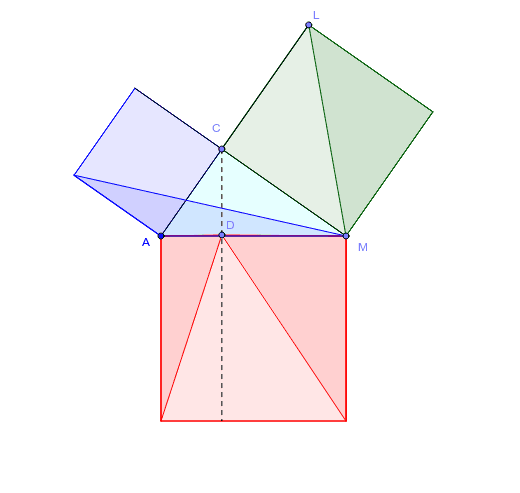
ピタゴラスの定理 ユークリッドの証明 Geogebra

三平方の定理の証明 相似な三角形を使う方法 数学教材
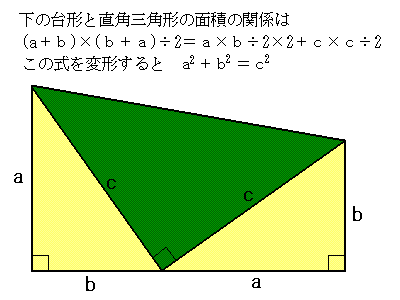
三平方の定理

三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト

必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ
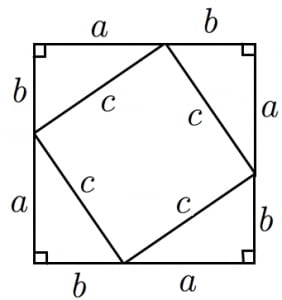
三平方の定理の4通りの美しい証明 高校数学の美しい物語
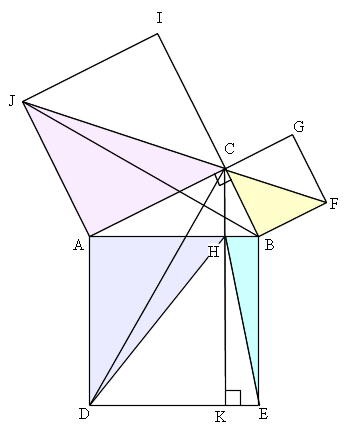
Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ

Ntuqjuuw5kkkbm
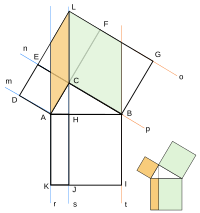
ピタゴラスの定理 Wikipedia 数学の定理まとめ Naver まとめ
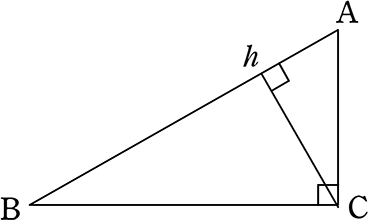
中学数学 三平方の定理

数学にとって証明とはなにか ピタゴラスの定理からイプシロン デルタ論法まで ブルーバックス 瀬山士郎 数学 Kindleストア Amazon
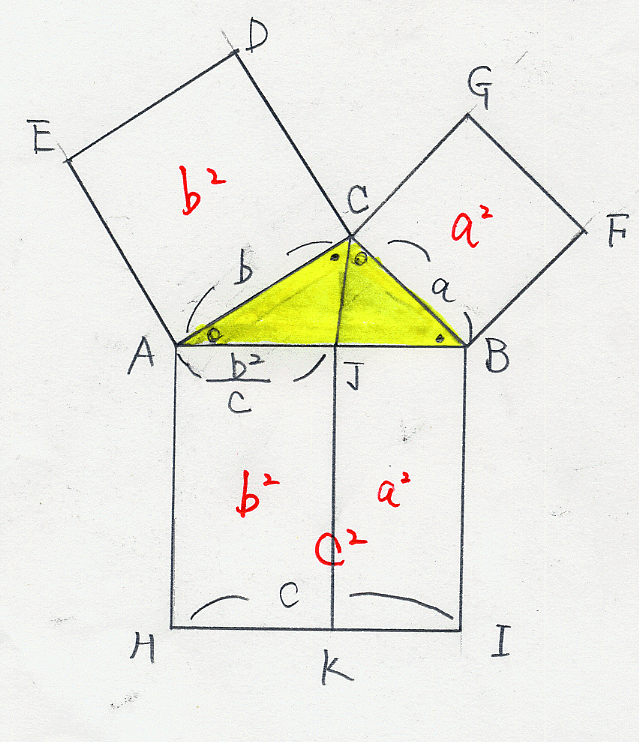
三平方の定理の逆の証明
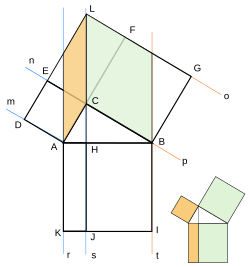
ピタゴラスの定理 Wikipedia

証明にこだわる

三平方の定理の証明 正方形の面積を使う方法 数学教材
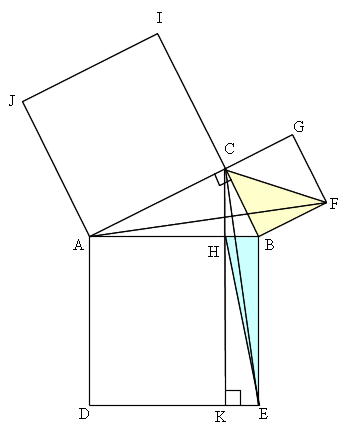
Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ

三平方の定理 ピタゴラスの定理 と証明 Rike English

三平方の定理とは 証明方法や例題についても解説 スタモ 受験 入試 学習の総合サイト
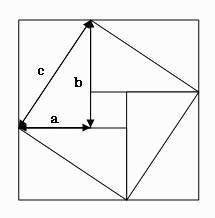
三平方の定理 ピタゴラスの定理 の歴史 素朴に考えてみよう
三平方の定理とは コトバンク

三平方の定理 ピタゴラスの定理 の例題や計算のやり方 証明 応用 難問などのまとめはこちらです 行間 ぎょうのあいだ 先生
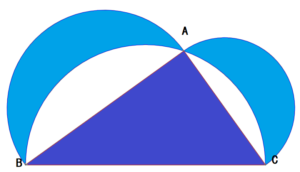
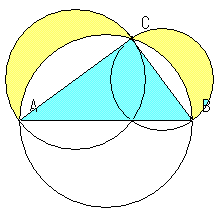
中学受験 ヒポクラテスの定理

ピタゴラスの定理 Wikipedia
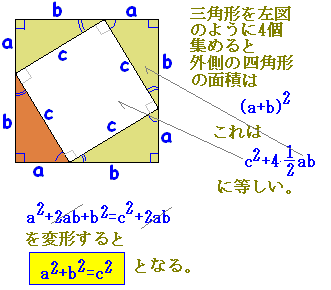
三平方の定理
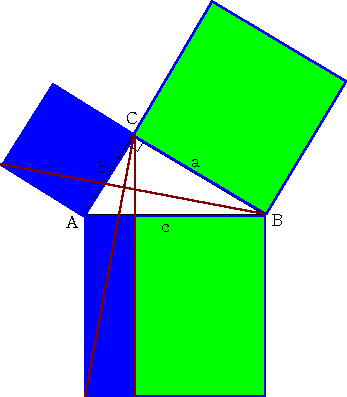
ピタゴラスの定理とその証明

三平方の定理の4通りの美しい証明 高校数学の美しい物語

三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ

3 4 5の三角形で 本当に直角ができる Note Board

カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 2 4

折り紙遊びは ピタゴラスの定理の証明 新 学力への挑戦 楽天ブログ




